How do you graph #(x+2)^2 + (y+3)^2 = 4#?
1 Answer
Aug 7, 2015
You determine the centre, vertices, and endpoints. Then you plot the graph.
Explanation:
This is the standard form for the equation of a circle with centre at (
This means that, to find the vertices, you go 2 units up from the centre and 2 units down.
Thus, the vertices are at (
To find the endpoints, you go 2 units left of the centre and 2 to the right.
Thus, the endpoints are at (
Plot the centre , the vertices, and the endpoints on a graph.
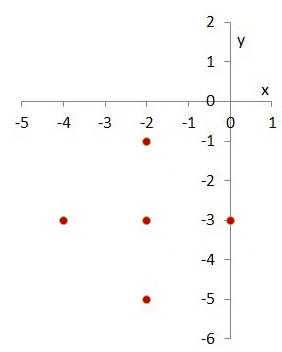
Now draw a smooth circle through the four outer points.
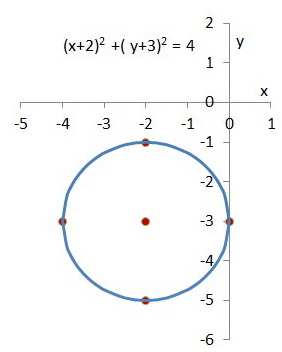
And you have your graph.

