Question

How do you identity if the equation `4x^2+2y^2=8` is a parabola, circle, ellipse, or hyperbola and how do you graph it?

Answer 1

The reference for Conic Section - General Cartesian form tells you how to determine what conic section it is.

Explanation:

The reference for Conic Section - General Cartesian form tells you how to determine what conic section it is, when given the General Cartesian form:

`Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0`

Here is the given equation in the general form:

`2x^2 + 4y^2 - 8 = 0`

Please observe the value of `B^2 - 4AC = 0^2 - 4(2)(4) = -32`. The reference says that this is an ellipse.

Divide both sides of the original equation by 8:

`x^2/4 + y^2/2 = 1`

Write the denominators as squares:

`x^2/2^2 + y^2/(sqrt(2))^2 = 1`

Insert zeros within the squares in the numerators:

`(x - 0)^2/2^2 + (y - 0)^2/(sqrt(2))^2 = 1`

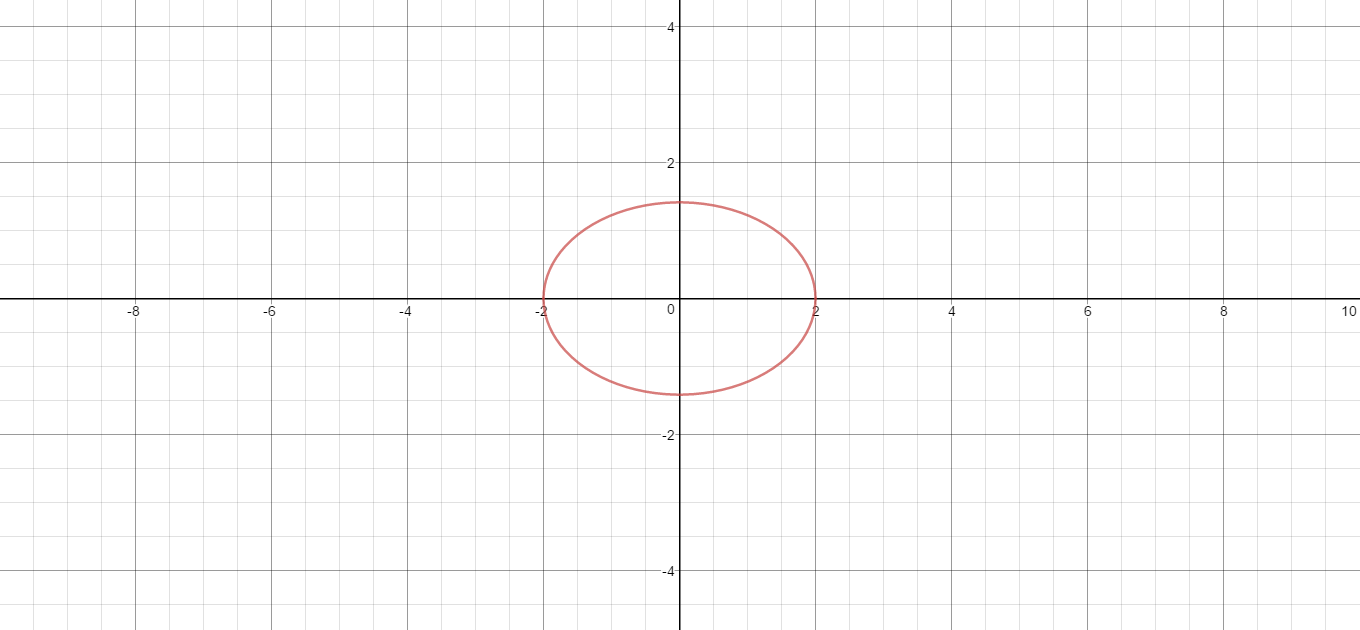
This is the standard form for an ellipse, because it is easy to see:

1. The center is (0, 0)
2. When `y = 0, x = -2 and 2`
3. When `x = 0, y = -sqrt(2) and sqrt(2)`

You may use these four points to graph the equation:

`(2, 0), (0, sqrt(2)), (-2, 0), and (0,-sqrt(2))`

And then sketch in an ellipse around the center.

Here is a graph of the equation: