Question

Cups A and B are cone shaped and have heights of `25 cm` and `15 cm` and openings with radii of `7 cm` and `3 cm`, respectively. If cup B is full and its contents are poured into cup A, will cup A overflow? If not how high will cup A be filled?

Answer 1

Cup A will be filled `12"cm"` high.

Explanation:

First, we calculate the volume of cup B.

`V_B=1/3pir_b^2*h=1/3pi*(3"cm")^2*15"cm"=45pi"cm"^3`

Both the height and radius of cup A are greater than those of cup B, so `V_a>V_b`. Hence, cup A will not overflow.

The image below represents cup A with cup B's full content. `V_("water")` is the volume of the water and `h_("water")` is the height of the water.

`V_("water")=1/3pi*r_("water")^2*h_("water")`

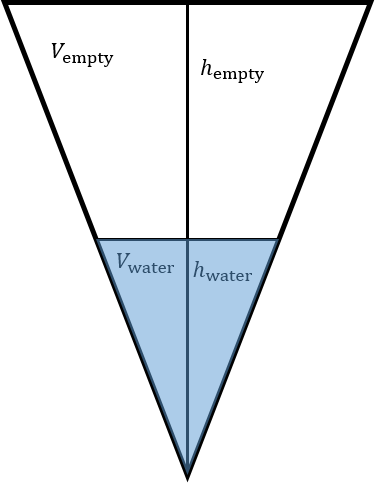The 'water triangle' is similar to cup A, so `hpropr`. This gives:

`V_("water")=1/3pi*(r_A*h_("water")/h_A)^2*h_("water")`
`V_("water")=1/3pi*r_A^2/h_A^2*h_("water")^3`
`V_("water")=(r_A^2pi)/(3h_A^2)*h_("water")^3`

`V_("water")=V_B`
`(r_A^2pi)/(3h_A^2)*h_("water")^3=45pi"cm"^3`
`h_("water")^3=(45pi"cm"^3)/((r_A^2pi)/(3h_A^2))=(135h_A^2)/(r_A^2)"cm"^3`
`h_("water")=root(3)((135"cm"^3*h_A^2)/(r_A^2))=root(3)((135"cm"^3*(25"cm")^2)/((7"cm")^2))~~12"cm"`

Cup A will therefore be filled `12"cm"` high.