How does the normal distribution relate to the real world?
1 Answer
Well, the reality is that a lot of data does have a normal distribution in the real world, if measurements/testing is done over a great enough period of time.
Explanation:
Normal distribution can and is actually achieved in many scientific studies. Whether you're looking at what time box turtles emerge in the spring, what age most children get chickenpox, or how long it takes a person to complete a college degree, the majority of your responses or answers are likely to be similar to one another (most box turtles emerge around the same time, most kids get chicken pox at the same time, most people take the same amount of time to finish a degree). Really outrageous or weird outcomes/measurements/answers are less likely.
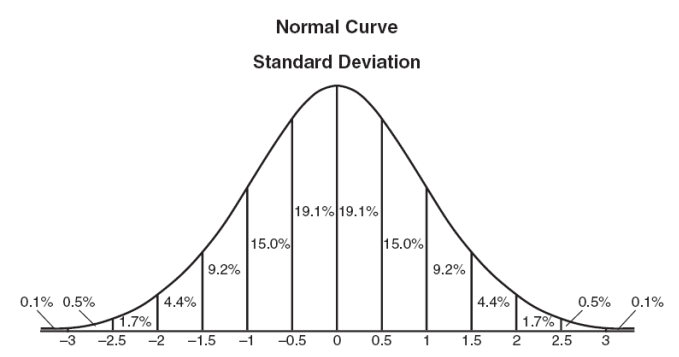
Using the college degree example, most people probably take four or five years to finish their college degree. In the normal distribution curve above, if the mean is 4.5 years, most people finish around that time. (Note: the numbers on the x axis are do not represent years, they represent the standard deviation.)
Some people may finish in three years and some may take longer: six or seven years. You may have a few people who finish in under two years or take a very, very long time to finish their degree. These data points are outliers though or very rare. The majority of people will finish in four or five years.
The main point is, if your sample size is large enough, your data will often closely fit a standard distribution curve. It may not fit it exactly, but it will fit it close enough that you can use parametric statistics (statistics deigned in part for when your data fits a normal distribution).

