Question

Question #8adc6

Answer 1

Here's what I got.

Explanation:

!! VERY LONG ANWER !!

`color(red)(!!!)color(white)(a)`SIDE NOTE There is something wrong with the values you provided, either for the mass of the sample or for the masses of carbon dioxide and water produced by the reaction.

My guess would be that the mass of the sample is actually `"2.416 g"`, not `"2.146 g"`. I will do the calculations using your values first, then solve the problem using (what I think is) accurate data.

The idea here is that you need to use the molar mass of the compound to determine how many moles you get in that `"2.146-g"` sample.

The molar masses of carbon dioxide and water will then help you determine how many moles of carbon and hydrogen were present in the given sample of dieldrin.

Once you know that, you can use the `2:1` mole ratio that exists between carbon and chlorine to find the number of moles of chlorine, and implicitly, the number of moles of oxygen present in the sample.

So, dieldrin has a molar mass of `"381 g mol"^(-1)`, which means that one mole of dieldrin has a mass of `"381 g"`. Your `"2.146-g"` sample will thus contain

`2.146color(red)(cancel(color(black)("g"))) * "1 mole dieldrin"/(381color(red)(cancel(color(black)("g")))) = "0.0056325 moles dieldrin"`

Now, use the molar mass of carbon dioxide to find how many moles of carbon dioxide were produced by the combustion reaction

`3.350color(red)(cancel(color(black)("g"))) * "1 mole CO"_2/(44.01color(red)(cancel(color(black)("g")))) = "0.076119 moles CO"_2`

Since one mole of carbon dioxide contains one mole of carbon and two moles of oxygen, this much carbon dioxide will contain

`n_(C) = 1 xx n_(CO_2) = "0.076119 moles C"`

To the same for water. You know that the combustion reaction produced

`0.458color(red)(cancel(color(black)("g"))) * ("1 mole H"_2"O")/(18.015color(red)(cancel(color(black)("g")))) = "0.025423 moles H"_2"O"`

Since one mole of water contains two moles of hydrogen and one mole of oxygen, this much water will contain

`n_(H) = 2 xx n_(H_2O) = 2 xx "0.025423 moles" = "0.050846 moles H"`

Now, all the moles of carbon that were initially present in the sample of dieldrin are now a part of the produced carbon dioxide. The same goes for all the moles of hydrogen, which are now a part of the produced water.

Since you know that dieldrin contains two moles of carbon for very one mole of chlorine, you can say that the sample contained

`n_(Cl) = 1/2 xx n_(C) = 1/2 * "0.076119 moles" = "0.038060 moles Cl"`

This means that the initial sample, i.e. `0.0056325` moles of dieldrin, also contained

• `0.076119` moles of carbon
• `0.050846` moles of hydrogen
• `0.038060` moles of chlorine

For now, don't worry about the number of moles of oxygen.

A compound's molecular formula tells you exactly how many moles of each constituent element you get in one mole of said compound.

In your case, one mole of dieldrin will contain

`1color(red)(cancel(color(black)("mole dieldrin"))) * "0.076119 moles C"/(0.0056325color(red)(cancel(color(black)("moles dieldrin")))) = "13.51 moles C" ->` NOT possible

At this point, you should stop because something is definitely wrong here.

Remember, one mole of a compound contains the exact number of moles of each constituent element.

In other words, the molecular formula will always tell you exactly how many atoms of each element you have in one molecule of compound.

This implies that you're looking for whole numbers here, since you cannot have fractions of an atom in a molecule.

MY VERSION OF THE PROBLEM

Now, look what happens if you start with `"2.416 g"` of dieldrin. The number of moles present in the sample will be

`2.416color(red)(cancel(color(black)("g"))) * "1 mole dieldrin"/(381color(red)(cancel(color(black)("g")))) = "0.0063412 moles dieldrin"`

Assuming that you still get `"3.350 g"` of carbon dioxide and `"0.458 g"` of water, the number of moles of carbon, hydrogen, and chlorine present in the sample will be the same as before.

However, the number of moles of each element present in one mole of dieldrin will be

`1color(red)(cancel(color(black)("mole dieldrin"))) * "0.076119 moles C"/(0.0063412color(red)(cancel(color(black)("moles dieldrin")))) = 12.004 ~~ "12 moles C"`

This result makes sense, since you're looking at a whole number of moles of carbon per mole of dieldrin.

Do the same for hydrogen and chlorine

`1color(red)(cancel(color(black)("mole dieldrin"))) * "0.050846 moles H"/(0.0063412color(red)(cancel(color(black)("moles dieldrin")))) = 8.02 ~~ "8 moles H"`

`1color(red)(cancel(color(black)("mole dieldrin"))) * "0.038060 moles Cl"/(0.0063412color(red)(cancel(color(black)("moles dieldrin")))) = 6.002 ~~ "6 moles Cl"`

To get the number of moles of oxygen present in one mole of dieldrin, use the compound's molar mass. You know that you must have

`12 xx "12.011 g mol"^(-1) ->` carbon's contribution to the molar mass of dieldrin

`8 xx "1.00794 g mol"^(-1) ->` hydrogen's's contribution to the molar mass of dieldrin

`6 xx "35.453 g mol"^(-1) ->` chlorine's contribution to the molar mass of dieldrin

`n_(O) xx "15.9994 g mol"^(-1) ->` oxygen's contribution to the molar mass of dieldrin
`color(white)(aaaaaaaaaa)/(color(white)(aaaaaaaaaaaaaaaaaaaa)`
`"381 g mol"^(-1) ->` the molar mass of dieldrin

This means that you have

`n_(O) = ((381 - 364.91) color(red)(cancel(color(black)("g mol"^(-1)))))/(15.9994color(red)(cancel(color(black)("g mol"^(-1))))) = 1.006 ~~ "1 mole O"`

Therefore, the molecular formula of dieldrin will be

`color(green)(|bar(ul(color(white)(a/a)"C"_12"H"_8"Cl"_6"O"color(white)(a/a)|)))`

Here's how the dieldrin molecule looks like

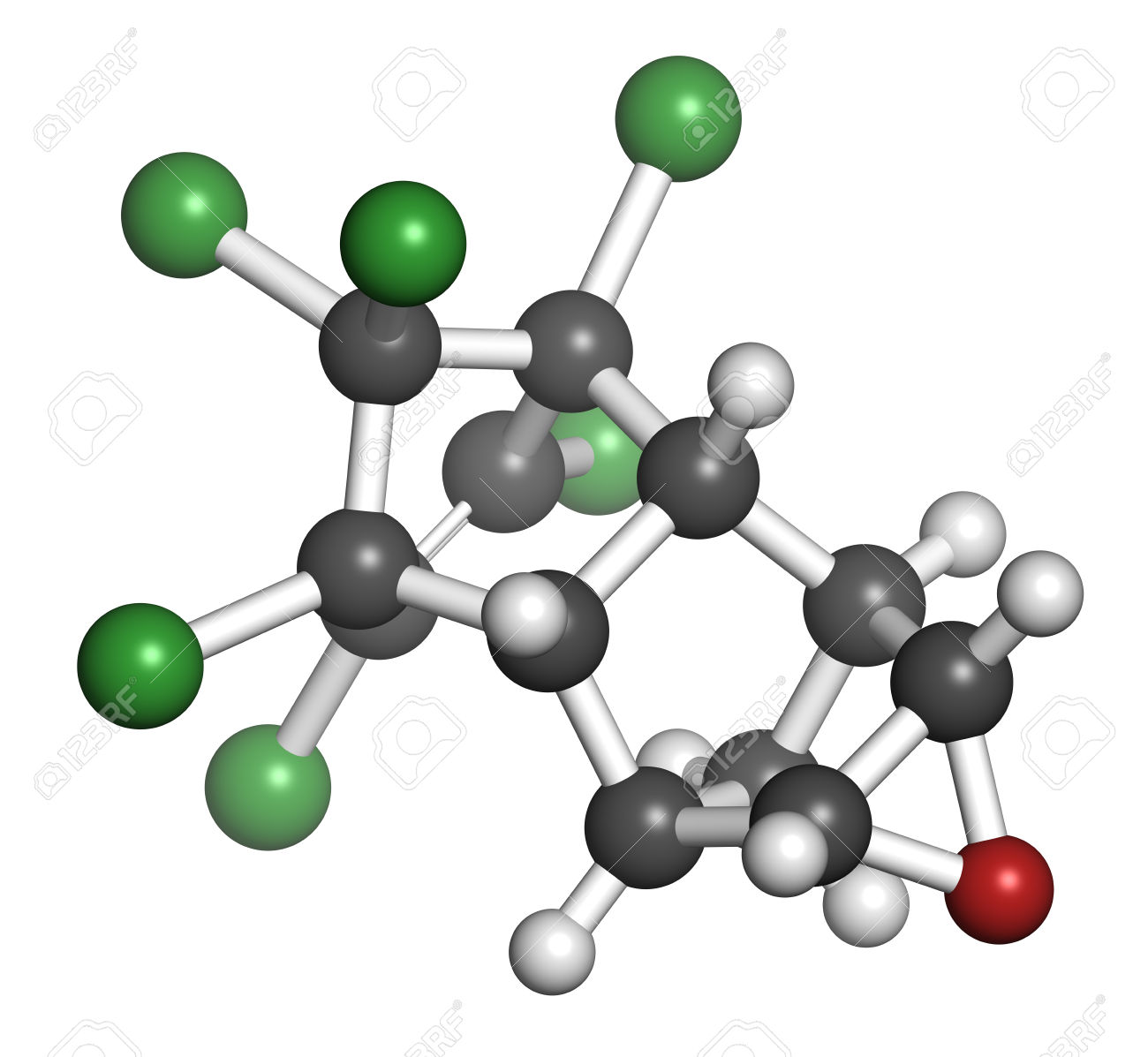
The carbon atoms are shown in black, the hydrogen atoms are shown in light gray, the chlorine atoms in green, and the oxygen atom in red.