Question #4ef82

Question

2101 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-02-05T08:29:19

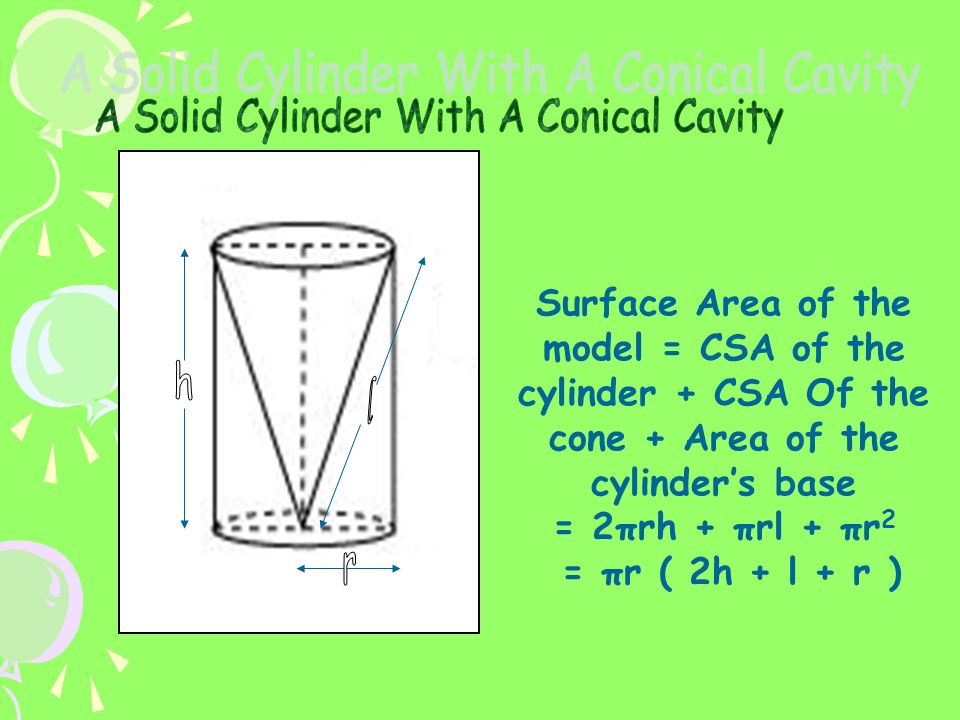
slideplayer.com

It is revealed from the above figure that surface area of the cyndrical solid with a conical cavity will be

$A = 2 π r h + π r l + π r^{2}$ $A=2pirh+pirl+pir^2$

$\Rightarrow A = π r (2 h + l + r)$ $=>A=pir(2h+l+r)$

Given
Total surface area of the solid $A = 904.32 d m^{2}$ $A=904.32dm^2$
Height of the solid $h = 16 d m$ $h=16dm$

Radius $r = 6 d m$ $r=6dm$

Density $ρ = 7.5 g / c m^{3} = 7.5 k g / d m^{3}$ $rho=7.5g"/"cm^3=7.5kg"/"dm^3$

The slant height $(l)$ $(l)$ of the cone is not known.

So
$904.32 = 3.14 \times 6 (2 \times 16 + l + 6)$ $904.32=3.14xx6(2xx16+l+6)$

$\Rightarrow l + 38 = \frac{904.32}{3.14 \times 6} = 48$ $=>l+38=(904.32)/(3.14xx6)=48$

$\Rightarrow l = 48 - 38 = 10 d m$ $=>l=48-38=10dm$

So height of the conical cavity will be

$h_{cone} = \sqrt{l^{2} - r^{2}}$ $h_"cone"=sqrt(l^2-r^2)$

$\Rightarrow h_{cone} = \sqrt{10^{2} - 6^{2}} = 8 d m$ $=>h_"cone"=sqrt(10^2-6^2)=8dm$

Now volume of the solid

$V = volume of cylinder - volume of cavity$ $V="volume of cylinder"-"volume of cavity"$

$= π r^{2} h - \frac{1}{3} π r^{2} h_{cone}$ $=pir^2h-1/3pir^2h_"cone"$

$= π r^{2} (h - \frac{h_{cone}}{3})$ $=pir^2(h-h_"cone"/3)$

So weight (mass) of the solid will be

$W = V \times ρ$ $W=Vxxrho$

$\Rightarrow W = V \times ρ = π r^{2} (h - \frac{h_{cone}}{3}) ρ$ $=>W=Vxxrho=pir^2(h-h_"cone"/3)rho$

$\Rightarrow W = 3.14 \times 6^{2} (16 - \frac{8}{3}) \times 7.5 k g$ $=>W=3.14xx6^2(16-8/3)xx7.5kg$

$\Rightarrow W = 3.14 \times 36 \times \frac{40}{3} \times 7.5 k g = 11304 k g$ $=>W=3.14xx36xx40/3xx7.5kg=11304kg$