Question

Question #5f823

Answer 1

`"0.180 M"`

Explanation:

The idea here is that you need to use the underlying principle of a dilution, which tells you that the concentration of a solution can be decreased by

• keeping the number of moles of solute constant
• increasing the volume of the solution


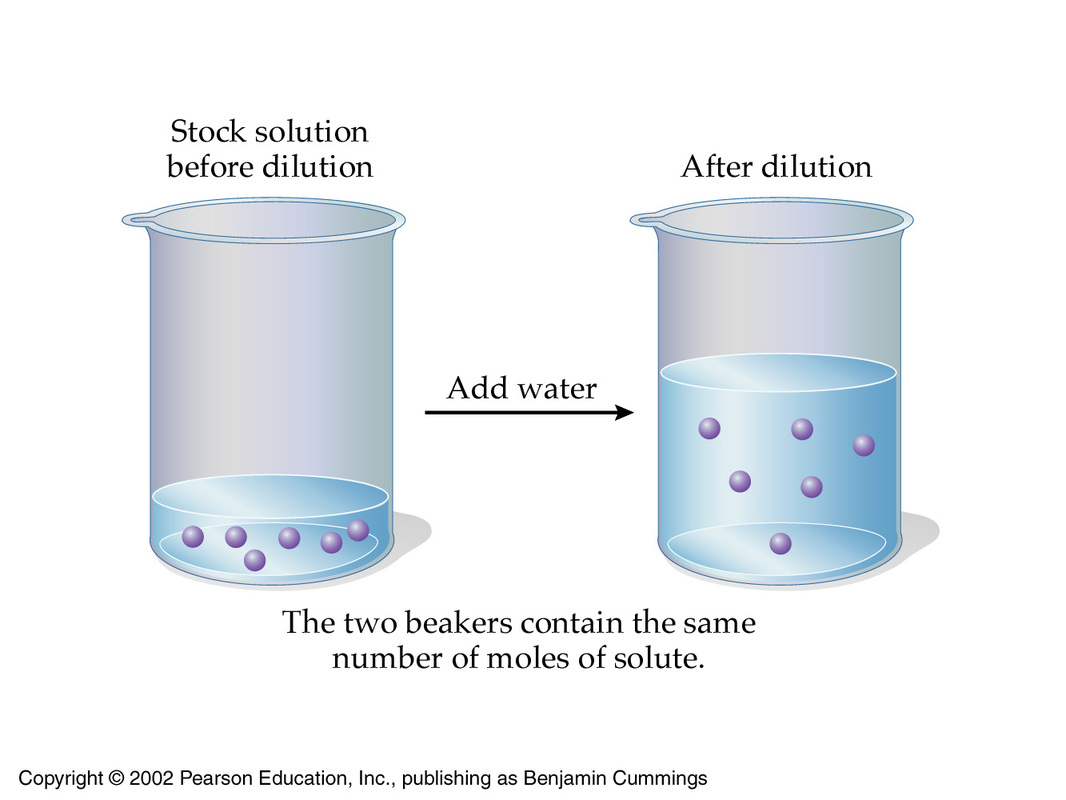
Mathematically, this can be expressed by using the molarities and volumes of the stock solution, which is the solution you're starting with, and the of the target solution

`color(blue)(overbrace(c_1 xx V_1)^(color(darkgreen)("moles of solute in concentrated solution")) = overbrace(c_2 xx V_2)^(color(darkgreen)("moles of solute in diluted solution"))`

Here

`c_1`, `V_1` - the molarity and volume of the concentrated solution
`c_2`, `V_2` - the molarity and volume of the diluted solution

So, your starting solution has a volume of `"100.0 mL"` and a molarity of `"1.35 M"`

`{(V_1 = "100.0 mL"), (c_1 = "1.35 M"):}`

The volume of the target solution will include the added water

`V_2 = "100.0 mL" + "650.0 mL" = "750.0 mL"`

Rearrange the above equation to solve for `c_2`, the concentration of the target solution, i.e. of the diluted solution.

`c_1V_1 = c_2V_2 implies c_2 = V_1/V_2 * c_1`

Plug in your values to find

`c_2 = (100.0 color(red)(cancel(color(black)("mL"))))/(750.0color(red)(cancel(color(black)("mL")))) * "1.35 M" = color(green)(|bar(ul(color(white)(a/a)color(black)("0.180 M")color(white)(a/a)|)))`

The answer is rounded to three sig figs.