How do you convert $2=(-x-3y)^2-5y+7x$ into polar form?

Question

1625 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-04-02T19:53:58

Substitute $rcos(theta)$ for x and $rsin(theta)$ for y and then simplify to a quadratic in r.
Use the positive root of the quadratic formula

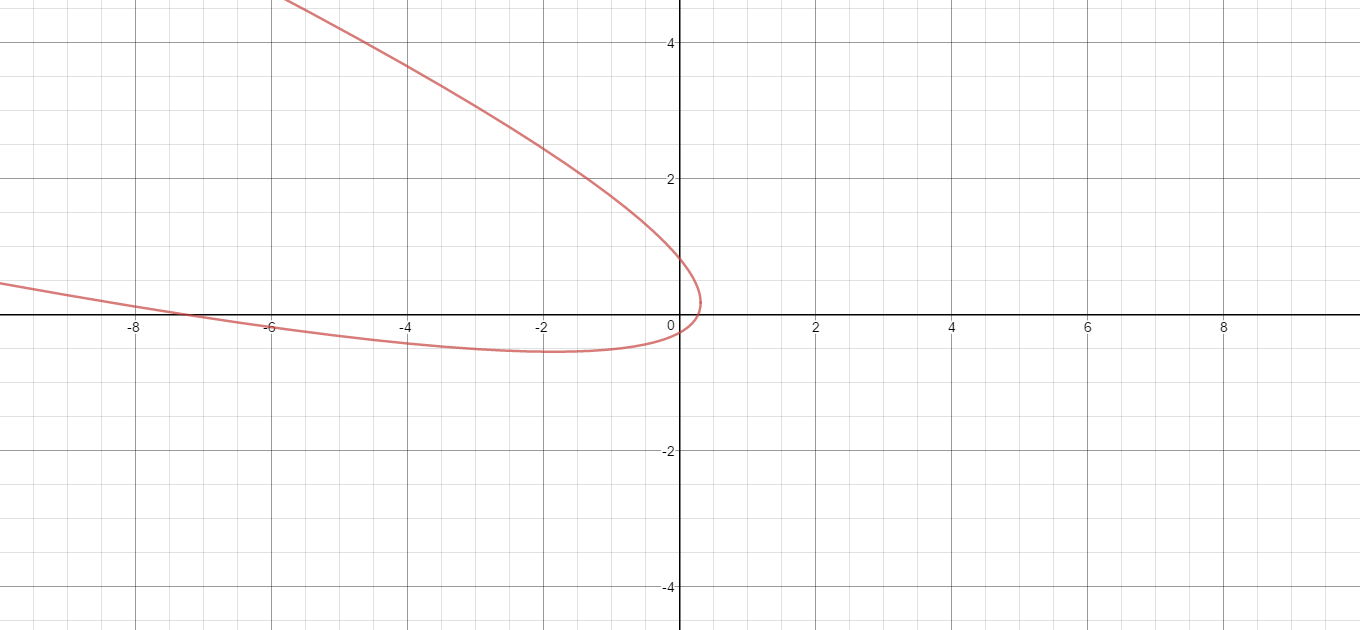
Given: $2=(-x-3y)^2-5y+7x$

Here is the graph of the Cartesian equation.

![Desmos.com]( useruploads.socratic.org )

Substitute $rcos(theta)$ for x and $rsin(theta)$ for y:

$2=(-rcos(theta)-3rsin(theta))^2-5rsin(theta)+7rcos(theta)$

Simplify:

$2=((-1)(r)(cos(theta)+3sin(theta)))^2+7rcos(theta)-5rsin(theta)$

$2=(-1)^2(r)^2(cos(theta)+3sin(theta))^2+(7cos(theta)-5sin(theta))r$

$0=(cos(theta)+3sin(theta))^2(r)^2+(7cos(theta)-5sin(theta))r -2$

$0=(cos(theta)+3sin(theta))^2r^2+ (7cos(theta)-5sin(theta))r - 2$

The above is a quadratic where $a = (cos(theta)+3sin(theta))^2, b = 7cos(theta)-5sin(theta) and c = -2$

Using the positive root of the quadratic formula:

$r = (5sin(theta)-7cos(theta) + sqrt((7cos(theta)-5sin(theta))^2+8(cos(theta)+3sin(theta))^2))/(2(cos(theta)+3sin(theta))^2)$

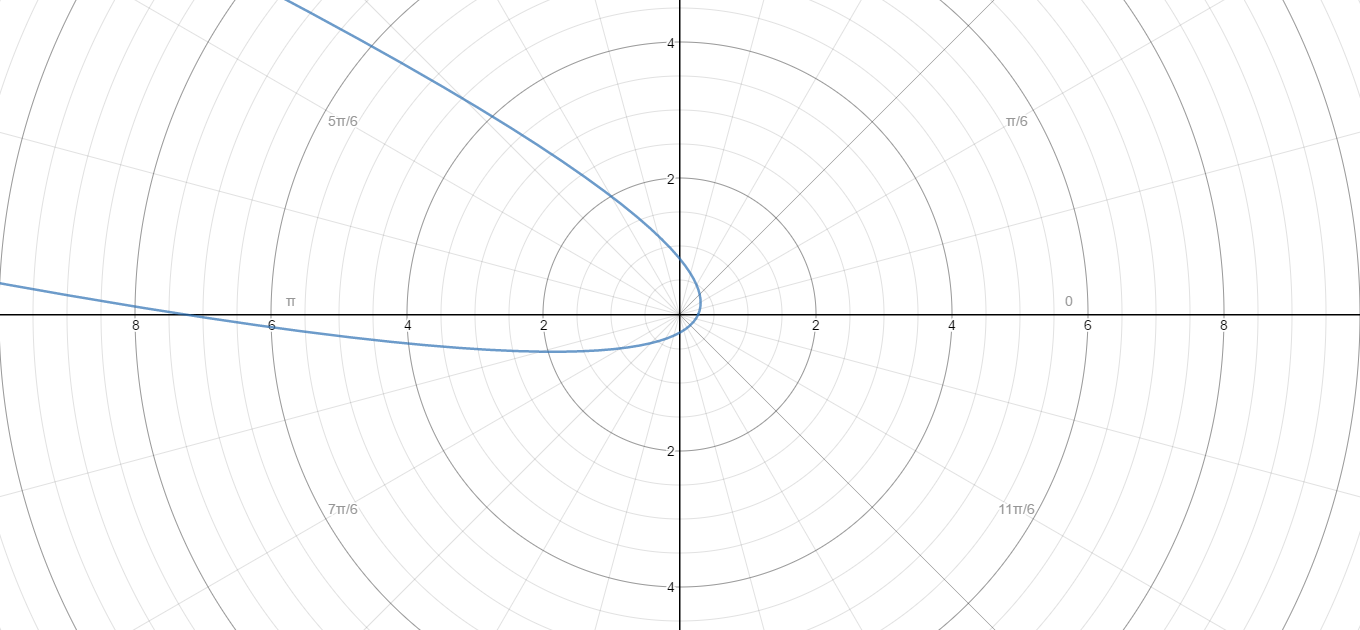
This is the polar equation.

Here is the graph of the polar equation

![Desmos.com]( useruploads.socratic.org )

This proves that the conversion is correct.

How do you convert 2=(-x-3y)^2-5y+7x2=(-x-3y)^2-5y+7x into polar form?