How do you find the critical points to graph $f (x) = 4 sin (x - \frac{π}{2})$ $f(x) = 4 sin(x -pi/2 )$ ?

Question

How do you find the critical points to graph $f (x) = 4 sin (x - \frac{π}{2})$ $f(x) = 4 sin(x -pi/2 )$ ?

1 Answer

Impact of this question

6445 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-12-12T20:36:48

$(\frac{π}{2}, 0)$ $(pi/2,0)$ , $(π, 4)$ $(pi,4)$ , $(\frac{3 π}{2}, 0)$ $((3pi)/2,0)$ , $(2 π, - 4)$ $(2pi,-4)$ , $(\frac{5 π}{2}, 0)$ $((5pi)/2,0)$

Explanation:

By the five-point method, you need five points to graph the function, $f (x) = 4 sin (x - \frac{π}{2})$ $f(x)=4sin(x-pi/2)$ . To find the five points, first find the five points for its parent function $e (x) = sin x$ $e(x)=sinx$ . Ignore the negative x values and its corresponding y values in the table below.

![ bscstudent.buffalostate.edu )

Now that you have the five points for the parent function, use the mapping rule to apply transformations in order to find the five points for the transformed function, $f (x) = 4 sin (x - \frac{π}{2})$ $f(x)=4sin(x-pi/2)$ .

Mapping rule: $(x + \frac{π}{2}, 4 y)$ $(x+color(red)(pi/2),color(blue)4y)$

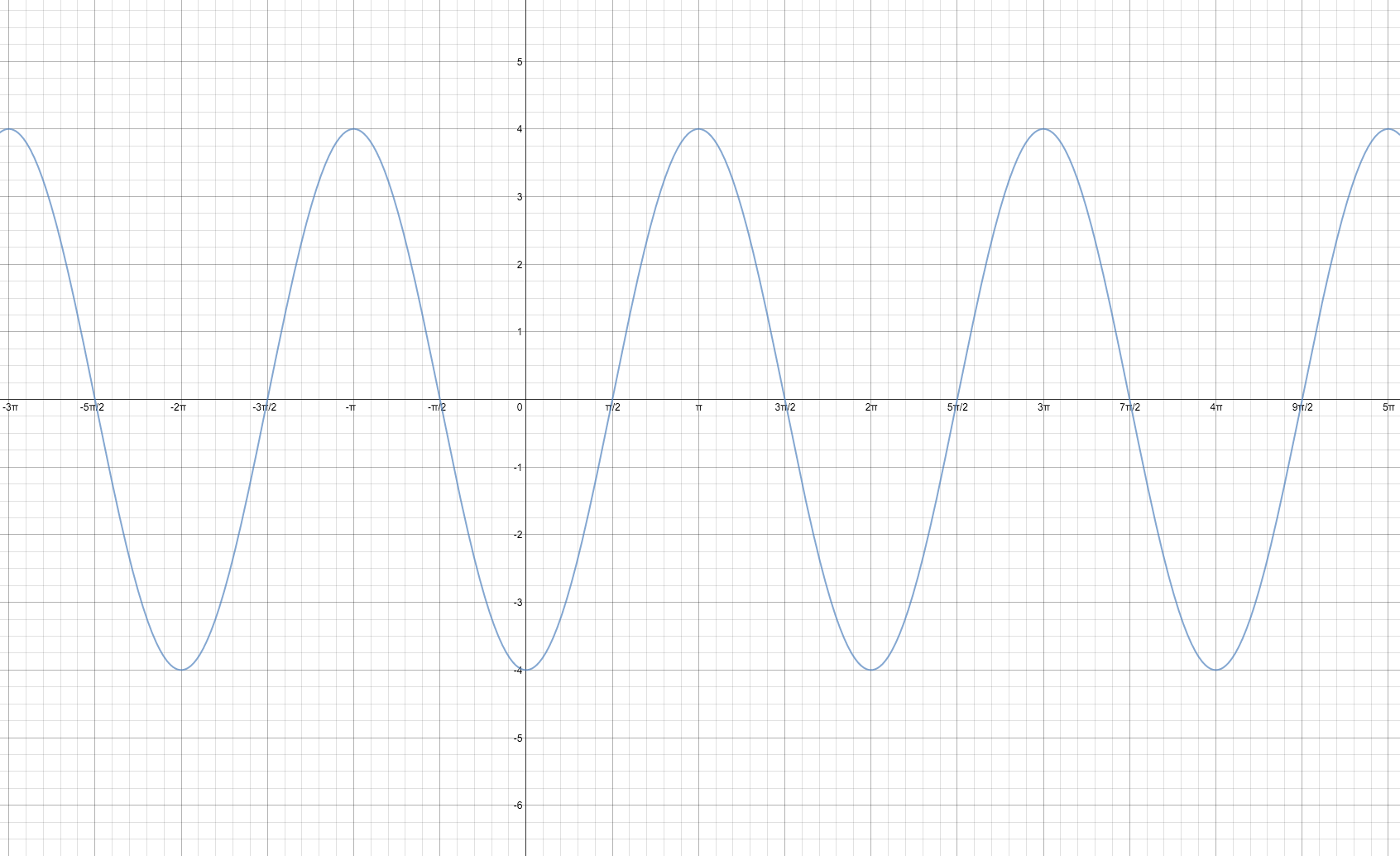
$f (x) = 4 sin (x - \frac{π}{2})$ $f(x)=4sin(x-pi/2)$
Point $1 . (0 + \frac{π}{2}, \times x (4) 0) \Rightarrow \times \times \times \times x (\frac{π}{2}, 0)$ $1. (0+color(red)(pi/2), color(white)(xxx)(color(blue)4)0) rArr color(white)(xxxxxxxxx)(pi/2,0)$
Point $2 . (\frac{π}{2} + \frac{π}{2}, \times (4) 1) \Rightarrow \times \times \times \times x (π, 4)$ $2. (pi/2+color(red)(pi/2), color(white)(xx)(color(blue)4)1) rArr color(white)(xxxxxxxxx)(pi,4)$
Point $3 . (π + \frac{π}{2}, \times x (4) 0) \Rightarrow a \times \times \times \times (\frac{3 π}{2}, 0)$ $3. (pi+color(red)(pi/2), color(white)(xxx)(color(blue)4)0) rArr color(white)(axxxxxxxx)((3pi)/2,0)$
Point $4 . (\frac{3 π}{2} + \frac{π}{2}, i x (4) (- 1)) \Rightarrow \times \times \times (2 π, - 4)$ $4. ((3pi)/2+color(red)(pi/2), color(white)(ix)(color(blue)4)(-1)) rArr color(white)(xxxxxx)(2pi,-4)$
Point $5 . (2 π + \frac{π}{2}, \times (4) 0) \Rightarrow \times \times \times \times x (\frac{5 π}{2}, 0)$ $5. (2pi+color(red)(pi/2), color(white)(xx)(color(blue)4)0) rArr color(white)(xxxxxxxxx)((5pi)/2,0)$

The transformed graph would look like:

![https://www.desmos.com/screenshot/6bf4rdat0g]( useruploads.socratic.org )

Zoom in to check the five main points shown on the graph.

Science

Math

Humanities

... and beyond

How do you find the critical points to graph $f (x) = 4 sin (x - \frac{π}{2})$ $f(x) = 4 sin(x -pi/2 )$ ?

1 Answer

Explanation:

Related questions

Impact of this question

Science

Math

Humanities

... and beyond

How do you find the critical points to graph f(x)=4sin(x−π2)f(x) = 4 sin(x -pi/2 )?

1 Answer

Explanation:

Related questions

Impact of this question

How do you find the critical points to graph $f (x) = 4 sin (x - \frac{π}{2})$ $f(x) = 4 sin(x -pi/2 )$ ?