When sketching angles in standard position, you must draw the initial side and the terminal side. The initial side is drawn on the positive xx-axis. The terminal side is drawn with the given angle measure away from the initial side.
)
The initial side represents an angle measure of 00. The positive yy-axis represents a measure of 90^@90∘ or (pi)/2π2 radians. The negative xx-axis represents a measure of 180^@180∘ or piπ radians. The negative yy-axis represents a measure of 270^@270∘ or (3pi)/23π2 radians. When you have an angle equivalent to 360^@360∘ or 2pi2π radians, the terminal side rests on the initial side.
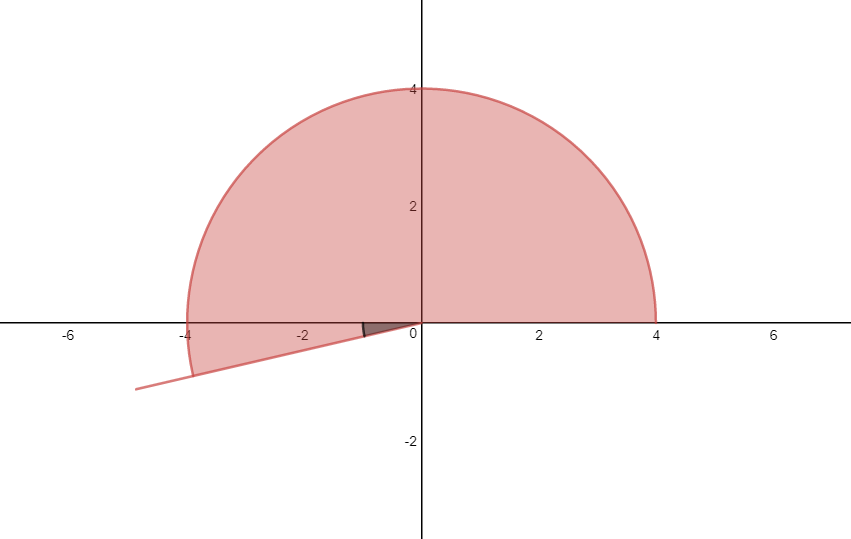
In this case, theta = 203^@θ=203∘ is between 180^@180∘ and 270^@270∘. Sketch it a little past the negative xx-axis, which represents 180^@180∘.
)
The reference angle is the acute angle made with the xx-axis and terminal side of the angle. In this case, the angle shaded in black is the reference angle. The reference angle is useful when trying to evaluate trigonometric ratios.
We can find its measure by calculating how far away it is from the xx-axis:
203^@ - 180^@ = 23^@203∘−180∘=23∘
