Question

How do you find the slope given `-3x + 8y = 24`?

Answer 1

`y = 3/8x + 3`

Explanation:

The easiest way to find the slope here is putting this in slope-intercept form, shown here:

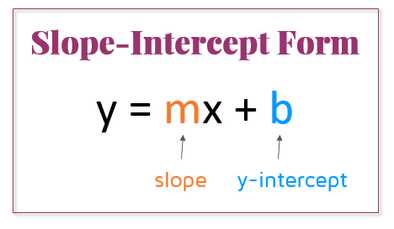
Following this image, let's change this equation. We need to make `y` by itself. To do so, first add `color(blue)(3x)` to both sides of the equation:
`-3x + 8y = 24`

`-3x + 8y quadcolor(blue)(+quad3x) = 24 quadcolor(blue)(+quad3x)`

`8y = 24 + 3x`

Now divide both sides by `color(blue)8`:
`(8y)/color(blue)8 = (24+3x)/color(blue)8`

Simplify to get `x` separated:
`y = 24/8 + 3/8x`

`y = 3 + 3/8x`

Match slope-intercept form:
`y = 3/8x + 3`

Now this matches slope-intercept form, meaning that `3/8` is the slope.

For more help on finding slope from standard form, feel free to watch this video:

Hope this helps!