Question

How do you graph `y = (x+3)^2-1`?

Answer 1

Find the vertex and axis of symmetry. Plot the vertex. Determine points on both sides of the axis of symmetry. Plot the points. Sketch a curve to represent the parabola. Do not connect the points.

Explanation:

`y=(x+3)^2-1` is in the vertex form of a parabola, `y=a(x-h)-1`, where `h=-3 and k=-1`.

First find the vertex. The vertex of the parabola is the point `(h,k)=(-3,-1)`. This is the highest or lowest point on the parabola.

Next find the axis of symmetry. The is the line `x=h=-3`. This is the line that separates the two halves of the parabola into mirror images.

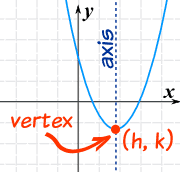
Now determine some points on both sides of the axis of symmetry by substituting values for `x` in the equation. Plot the vertex and the points. Sketch a graph that is a curved parabola. Do not connect the dots.

`x=-5,` `y=3`
`x=-4,` `y=0`
`x=-2,` `y=0`
`x=-1,` `y=3`

graph{y=(x+3)^2-1 [-10, 10, -5, 5]}