hat A = 102^@, b = 13, c = 10ˆA=102∘,b=13,c=10
We cannot directly use Law of Sines.
"First let's use Law of Cosines to find the third side " color(brown)(a)First let's use Law of cosines to find the third side a
useruploads.socratic.org)
a^2 = b^2 + c^2 - (2 b c cos A)a2=b2+c2−(2bccosA)
a = sqrt(13^2 + 10^2 - (2 * 13 * 10 * cos 102)) = 17.97 " units"a=√132+102−(2⋅13⋅10⋅cos102)=17.97 units
Only one triangle is possible, having " " hatA = 102^@ ˆA=102∘ an obtuse angle.
Since we know all the three sides and one angle, we can apply law of sines to find the other two angles.
sin A / a = sin B / b = sin C / csinAa=sinBb=sinCc
hat B = sin ^-1 ((b.sin A) / a) = sin^-1 ((13 * sin 102)/17.97) = 45.03^@ˆB=sin−1(b.sinAa)=sin−1(13⋅sin10217.97)=45.03∘
Similarly, hat C = sin _1 ((10 * sin 102) / 17.97) = 32.97^@ˆC=sin1(10⋅sin10217.97)=32.97∘
"Area of the triangle " A_t = (1/2) b c sin A = (1/2) * 13 * 10 * sin 102 = color(maroon)(63.58 " sq units"Area of the triangle At=(12)bcsinA=(12)⋅13⋅10⋅sin102=63.58 sq units
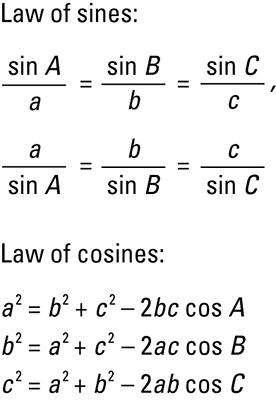