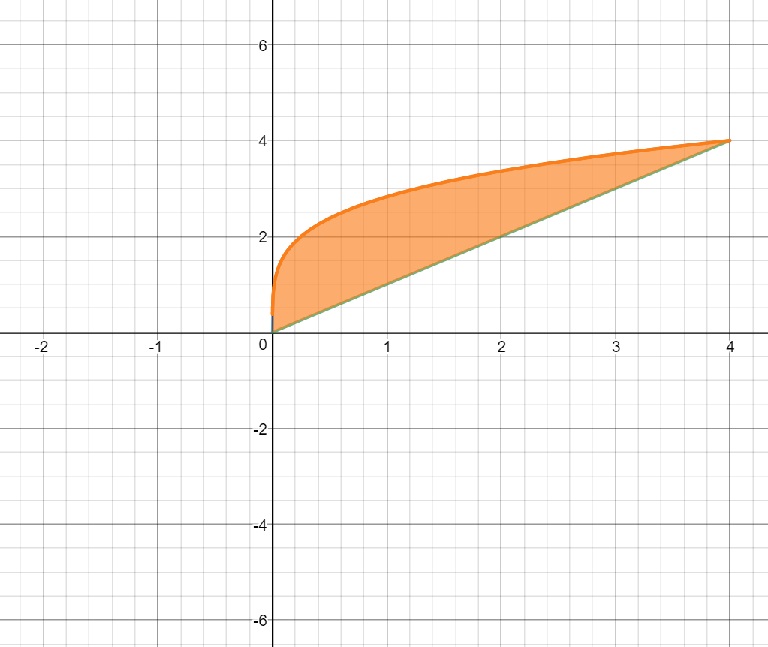
First, plot the two graphs, shading the bounded region between them.
 )
)
Second, recall the formula for solid of revolution about the #x#-axis
#int_(x_0)^(x_f)pi("outer radius")^2-pi("inner radius")2dx#
The outer radius is the height from the #x#-axis to the outer most graph, or #y=(64x)^(1/4)#
#int_(x_0)^(x_f)pi((64x)^(1/4))^2-pi("inner radius")^2dx#
The inner radius is the height from the #x#-axis to the inner most graph, or #y=x#
#int_(x_0)^(x_f)pi((64x)^(1/4))^2-pi(x)^2dx#
The lower limit of integration is the smallest #x#-value where the two curves meet, or #x_0=0#. The upper limit of integration is the largest #x#-value where the two curves meet, or #x_f=4#
#int_(0)^(4)pi((64x)^(1/4))^2-pi(x)^2dx#
#int_(0)^(4)pi(64x)^(1/2)-pix^2dx#
#int_(0)^(4)pi8x^(1/2)-pix^2dx#
#int_(0)^(4)pi8x^(1/2)dx-int_(0)^(4)pix^2dx#
#8piint_(0)^(4)x^(1/2)dx-piint_(0)^(4)x^2dx#
#16/3pi[x^(3/2)]_(0)^(4)-pi/3[x^3]_(0)^(4)#
#16/3pi(4)^(3/2)-pi/3(4)^3=(64pi)/3#
 )
) 