The coordinates of a polygon are (2, 3), (4,7), (8,5), and (7,2). If the polygon rotates 90° clockwise about the origin, in which quadrant will the transformation lie? What are the new coordinates?

Question

A) Quad II; (-2, 3), (-4,7), (-8,5), and (-7,2)
B) Quad IV; (3, -2), (7, -4), (5, -8), and (2, -7)
C) Quad III; (-2, -3), (-4,-7), (-8,-5), and (-7,-2)
D) Quad III: (-3, -2), (-7,-4)), (-5, -8), and (2, -7)

4425 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-03-29T07:37:42

B) All the four points and the polygon lie in the IV Quadrant

and the coordinates are #(3, -2), (7, -4), (5, -8), (2, -7)#

Given coordinates : #A (2,3), B (4,7), C (8,5), D (7,2)#

Presently, the polygon lies in the I Quadrant.

All the four points are rotated about the origin by #90^@ or (pi/2)^c#

#A (2,3) -> A' (3,-2)#

#B (4,7) -> B' (7, -4)#

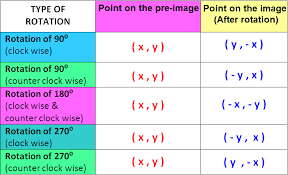
C (8, 5) -> C' (5, -8)#

#D (7,2) -> D' (2,-7)#

All the four points and the polygon lie in the IV Quadrant

and the coordinates are #(3, -2), (7, -4), (5, -8), (2, -7)#