To go from #v_1# to #v_2# the x coordinate decreased by 7 and the y coordinate decreased by 20.
To go from #v_1# to the center #(h, k)#, the x coordinate must decrease by 3.5 and the y coordinate must decrease by 10:
Therefore, #h = 1.5, k = 0,# and the center of the ellipse is #(1.5, 0)#
The length of the semi-major axis, a, is the distance from the center to either vertex:
#a = sqrt((5 - 1.5)^2 + (10 - 0)^2)#
#a = sqrt((3.5)^2 + 10^2)#
#a = sqrt(449)/2#
Let A = the angle of rotation, then:
#sin(A) = 10/(sqrt(449)/2), and cos(A) = 3.5/(sqrt(449)/2)#
Rationalizing both denominators:
#sin(A) = (20sqrt(449))/449 and cos(A) = (7sqrt(449))/449#
Here is a reference for An Rotated Ellipse that I not at the origin
#((x - h)cos(A) + (y - k)sin(A))^2/a^2 + ((x - h)sin(A) - (y - k)cos(A))^2/b^2 = 1#
Solving for #b#
#1 - ((x - h)cos(A) + (y - k)sin(A))^2/a^2= ((x - h)sin(A) - (y - k)cos(A))^2/b^2 #
#b^2 = (a^2((x - h)sin(A) - (y - k)cos(A))^2)/(a^2 - ((x - h)cos(A) + (y - k)sin(A))^2)#
#b = sqrt((a^2((x - h)sin(A) - (y - k)cos(A))^2)/(a^2 - ((x - h)cos(A) + (y - k)sin(A))^2))#
Force this to contain the point #(-5, -4)#:
#b = sqrt(((449/4)((-5 - 1.5)(20sqrt(449))/449 - (-4 - 0)(7sqrt(449))/449)^2)/((449/4) - ((-5 - 1.5)(7sqrt(449))/449 + (-4 - 0)(20sqrt(449))/449)^2))#
I used WolframAlpha to do the evaluation:
#b = 5.80553#
Here is the final equation:
#((x - 1.5)(20sqrt(449))/449 + (y - 0)(7sqrt(449))/449)^2/(sqrt(449)/2)^2 + ((x - 1.5)(7sqrt(449))/449 - (y - 0)(20sqrt(449))/449)^2/(5.80553)^2 = 1#
Here is a graph to prove it:
 )
)
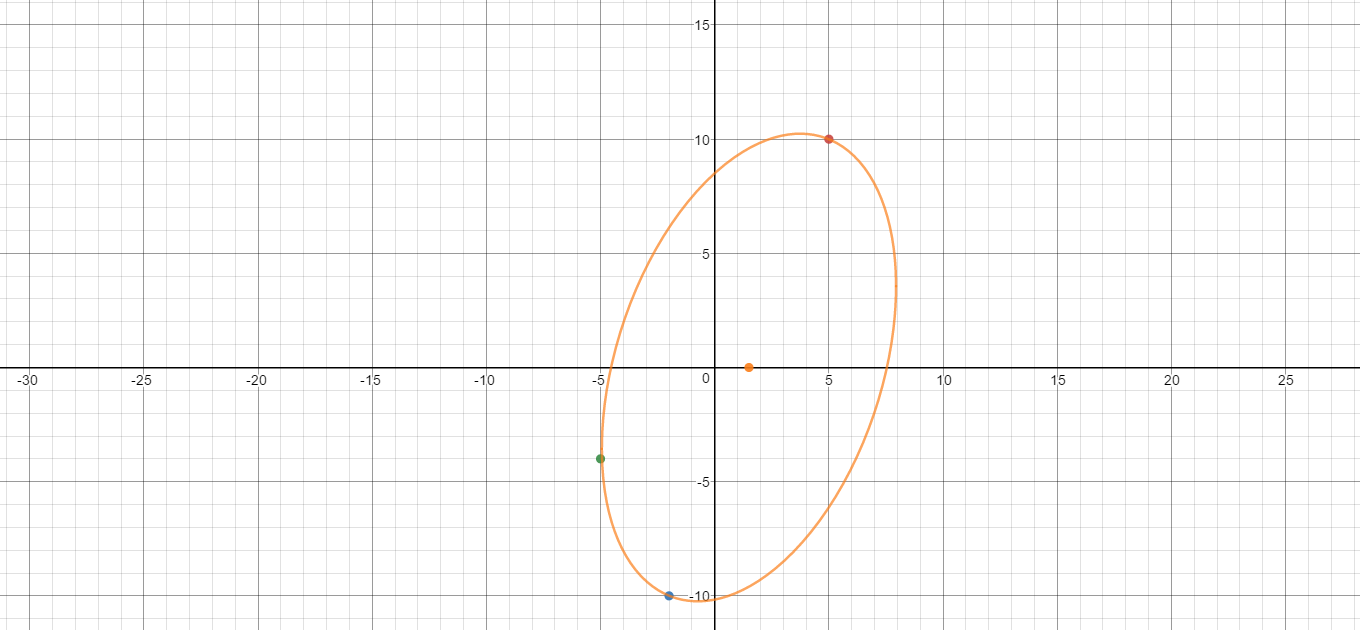 )
) 