Question

Why is the electron configuration of chromium `1s^2 2s^2 2p^6 3s^2 3p^6 3d^color(red)(5) 4s^color(red)(1)` instead of `1s^2 2s^2 2p^6 3s^2 3p^6 3d^color(red)(4) 4s^color(red)(2)`?

Answer 1

It's a combination of factors:

• Less electrons paired in the same orbital
• More electrons with parallel spins in separate orbitals
• Pertinent valence orbitals NOT close enough in energy for electron pairing to be stabilized enough by large orbital size

---

DISCLAIMER: Long answer, but it's a complicated issue, so... :)

A lot of people want to say that it's because a "half-filled subshell" increases stability, which is a reason, but not necessarily the only reason. However, for chromium, it's the significant reason.

It's also worth mentioning that these reasons are after-the-fact; chromium doesn't know the reasons we come up with; the reasons just have to be, well, reasonable.

The reasons I can think of are:

• Minimization of coulombic repulsion energy
• Maximization of exchange energy
• Lack of significant reduction of pairing energy overall in comparison to an atom with larger occupied orbitals

COULOMBIC REPULSION ENERGY

Coulombic repulsion energy is the increased energy due to opposite-spin electron pairing, in a context where there are only two electrons of nearly-degenerate energies.

So, for example...

`ul(uarr darr) " " ul(color(white)(uarr darr)) " " ul(color(white)(uarr darr))` is higher in energy than `ul(uarr color(white)(darr)) " " ul(darr color(white)(uarr)) " " ul(color(white)(uarr darr))`

To make it easier on us, we can crudely "measure" the repulsion energy with the symbol `Pi_c`. We'd just say that for every electron pair in the same orbital, it adds one `Pi_c` unit of destabilization.

When you have something like this with parallel electron spins...

`ul(uarr darr) " " ul(uarr color(white)(darr)) " " ul(uarr color(white)(darr))`

It becomes important to incorporate the exchange energy.

EXCHANGE ENERGY

Exchange energy is the reduction in energy due to the number of parallel-spin electron pairs in different orbitals.

It's a quantum mechanical argument where the parallel-spin electrons can exchange with each other due to their indistinguishability (you can't tell for sure if it's electron 1 that's in orbital 1, or electron 2 that's in orbital 1, etc), reducing the energy of the configuration.

For example...

`ul(uarr color(white)(darr)) " " ul(uarr color(white)(darr)) " " ul(color(white)(uarr darr))` is lower in energy than `ul(uarr color(white)(darr)) " " ul(darr color(white)(uarr)) " " ul(color(white)(uarrdarr))`

To make it easier for us, a crude way to "measure" exchange energy is to say that it's equal to `Pi_e` for each pair that can exchange.

So for the first configuration above, it would be stabilized by `Pi_e` (`1harr2`), but the second configuration would have a `0Pi_e` stabilization (opposite spins; can't exchange).

PAIRING ENERGY

Pairing energy is just the combination of both the repulsion and exchange energy. We call it `Pi`, so:

`Pi = Pi_c + Pi_e`

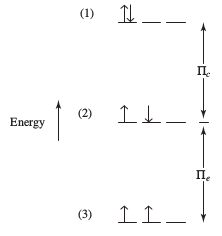
Basically, the pairing energy is:

• higher when repulsion energy is high (i.e. many electrons paired), meaning pairing is unfavorable
• lower when exchange energy is high (i.e. many electrons parallel and unpaired), meaning pairing is favorable

So, when it comes to putting it together for chromium... (`4s` and `3d` orbitals)

`ul(uarr color(white)(darr))`

`ul(uarr color(white)(darr)) " " ul(uarr color(white)(darr)) " " ul(uarr color(white)(darr)) " " ul(uarr color(white)(darr)) " " ul(uarr color(white)(darr))`

compared to

`ul(uarr darr)`

`ul(uarr color(white)(darr)) " " ul(uarr color(white)(darr)) " " ul(uarr color(white)(darr)) " " ul(uarr color(white)(darr)) " " ul(color(white)(uarr darr))`

is more stable.

For simplicity, if we assume the `4s` and `3d` electrons aren't close enough in energy to be considered "nearly-degenerate":

• The first configuration has `\mathbf(Pi = 10Pi_e)`.

(Exchanges: `1harr2, 1harr3, 1harr4, 1harr5, 2harr3,`
`2harr4, 2harr5, 3harr4, 3harr5, 4harr5`)

• The second configuration has `\mathbf(Pi = Pi_c + 6Pi_e)`.

(Exchanges: `1harr2, 1harr3, 1harr4, 2harr3, 2harr4, 3harr4`)

Technically, they are about `"3.29 eV"` apart (Appendix B.9), which means it takes about `"3.29 V"` to transfer a single electron from the `3d` up to the `4s`.

We could also say that since the `3d` orbitals are lower in energy, transferring one electron to a lower-energy orbital is helpful anyways from a less quantitative perspective.

COMPLICATIONS DUE TO ORBITAL SIZE

Note that for example, `"W"` has a configuration of `[Xe] 5d^4 6s^2`, which seems to contradict the reasoning we had for `"Cr"`, since the pairing occurred in the higher-energy orbital.

But, we should also recognize that `5d` orbitals are larger than `3d` orbitals, which means the electron density can be more spread out for `"W"` than for `"Cr"`, thus reducing the pairing energy `Pi`.

That is, `Pi_"W" < Pi_"Cr"`.

Since a smaller pairing energy implies easier electron pairing, that is probably how it could be that `"W"` has a `[Xe] 5d^4 6s^2` configuration instead of `[Xe] 5s^5 6s^1`; its `5d` and `6s` orbitals are large enough to accommodate the extra electron density.

Indeed, the energy difference in `"W"` for the `5d` and `6s` orbitals is only about `"0.24 eV"` (Appendix B.9), which is quite easy to overcome simply by having larger orbitals that stabilize the pairing energy.