First, let's look at those for the neutral atom, and then work our way to the cation.
VANADIUM (V)
#"V"# is atomic number #23#, so its configuration is #1s^2 2s^2 2p^6 3s^2 3p^6 3d^3 4s^2#. In shorthand it is #[Ar] 3d^3 4s^2#. This is an expected configuration; not an oddball element.
Since the #4s# orbital is higher in energy, its electrons will be removed first. Not that it matters here, though, because exactly #5# electrons are removed:
#color(blue)("V"^(5+) -> 1s^2 2s^2 2p^6 3s^2 3p^6 -= [Ar])#
GOLD (III)
#"Au"# is atomic number #79#, so its configuration is #1s^2 2s^2 2p^6 3s^2 3p^6 3d^10 4s^2 4p^6 4d^10 5s^2 5p^6 4f^14 5d^10 6s^1#. In shorthand it is #[Xe] 4f^14 5d^10 6s^1#.
This is strange, not only because gold wants to acquire a filled #5d# subshell, but more likely also something to do with the high amount of relativistic contraction effects; the #s# electrons move close to the speed of light and are often farther from the nucleus than closer, shrinking the radius of the #1s# orbital by #~22%#, and other orbitals by a bit as well.
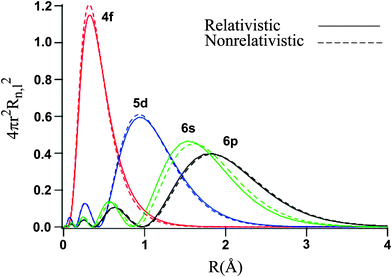
Let's examine the radial density distribution of the #6s#, #5d#, and #4f# valence orbitals to see how that turns out:
 )
)
By a long shot, the #4f# is the most penetrating, meaning that most of its electron density is centered near the gold nucleus. Further out are the #5d# electrons, and then the #6s# electrons.
This suggests that the #6s# orbital, which has most electron density farther out from the nucleus, has electron(s) that are less attracted to the nucleus (smaller #Z_(eff)#) than those in either the #5d# or #4f# orbitals, and thus contains the first electron that is easiest to remove during ionization.
The #5d# contains the next two electrons that will be removed during the second and third ionizations.
So, we would get:
#color(blue)("Au"^(3+) -> 1s^2 2s^2 2p^6 3s^2 3p^6 3d^10 4s^2 4p^6 4d^10 5s^2 5p^6 4f^14 5d^8 -= [Xe] 4f^14 5d^8)#
IRON (II)
#"Fe"# is atomic number #26#, so its configuration is #1s^2 2s^2 2p^6 3s^2 3p^6 3d^6 4s^2#. In shorthand it is #[Ar] 3d^6 4s^2#. This is an expected configuration; not an oddball element.
The first and second ionizations would removed the #4s# electrons, which are higher in energy than the #3d# electrons, so we get:
#color(blue)("Fe"^(2+) -> 1s^2 2s^2 2p^6 3s^2 3p^6 3d^6 -= [Ar] 3d^6)#
 )
) 
