Question

Question #d5b0c

Answer 1

`P=3sqrt3+9`

Explanation:

In a 30°-60°-90° triangle, with the side opposite the 30° angle being x, the sides would be `x, xsqrt3, 2x`, respectively (as shown below).

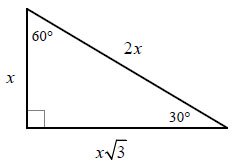
Given this, we know that the hypotenuse`=6`, and that the hypotenuse is opposite the 90° angle. We then get the equation:

`2x=6`

Divide by `2`

`x=3`

The perimeter of a triangle is the sum of all its sides. Since we know what `x` equals now, we can find the perimeter of this triangle.

`P=x+xsqrt3+2x`

Substitute `3` as `x`.

`P=3+3sqrt3+(2*3)`

`P=3+3sqrt3+6`

Add like terms (`3` and `6`).

`P=3sqrt3+9`