Question

Estimate the area under the curve `f(x) = x^2` over the interval `[0,10]` with `5` strips using Left Riemann Sums?

Answer 1

Since you are using 5 sub intervals, your intervals would be divided like this:
`[0,2], [2,4], [4,6], [6,8], [8,10]`

The left riemann sum requires you to use the lower number in every interval listed above as your `x` term, and then evaluate the functional value at that particular `x` value, like this:

Note that `2` would be the width of every rectangle formed, since the intervals are of equal width.

`1. Area_1 = f(0)*2 = 0^2*2 = 0`

`2. Area_2 = f(2)*2 = 2^2*2 = 8`

`3. Area_3 = f(4)*2 = 4^2*2 = 32`

`4. Area_4 = f(6)*2 = 6^2*2 = 72`

`5. Area_5 = f(8)*2 = 8^2*2 = 128`

Upon finding the individual areas of each of the five rectangles formed by the five sub-intervals evaluated at the "left side" `x` value, all that is left to do is add all the individual areas up:

`Total Area = 0 + 8 + 32 + 72 + 128 = 240`

Alternatively, you could use the fact that all the rectangles are the same width, keeping `Deltax` the same:
`Total Sum = 2*(f(0) + f(2) + f(4) + f(6) + f(8))`
`Total Sum = 2*(0 + 4 + 16 + 36 + 64) = 2*(120) = 240`

Therefore your left riemann sum would be `240` for the graph `y = x^2`on the interval `[0,10]`

Answer 2

`LRS = 240`

Explanation:

We have:

`f(x) = x^2`

We want to calculate over the interval `[0,10]` with `5` strips; thus:

`Deltax = (10-0)/5 = 2`

Note that we have a fixed interval (strictly speaking a Riemann sum can have a varying sized partition width). The values of the function are tabulated as follows;

Left Riemann Sum

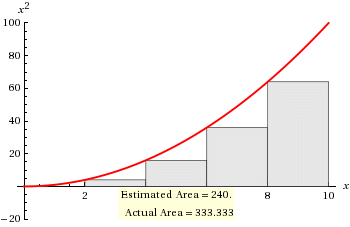
`LRS = sum_(r=0)^4 f(x_i) \ Deltax_i`
`" " = 2 * (0 + 4 + 16 + 36 + 64)`
`" " = 2 * (120)`
`" " = 240`

Actual Value

For comparison of accuracy:

`Area = int_0^10 \ x^2 \ dx`
`" " = [x^3/3]_0^10`
`" " = 1/3[x^3]_0^10`
`" " = 1/3(1000)`
`" " = 1000/3`
`" " = 333.3333...`