Assuming you are saying #(2x-3y)^9#,
Binomial Theorem states that #->#
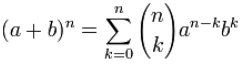
The first term's exponents start at n and go down
The second term's exponents start at 0 and go up ...
#color(red)((2x-3y)^9 = (2x)^9(-3y)^0+(2x)^8(-3y)^1+(2x)^7(-3y)^2+(2x)^6(-3y)^3+(2x)^5(-3y)^4+(2x)^4(-3y)^5+(2x)^3(-3y)^6+(2x)^2(-3y)^7+(2x)^1(-3y)^8+(2x)^0(-3y)^9)#
#=>color(blue)((2x-3y)^9 = 512x^9 + (256x^8)(-3y^1) + (128x^7)(9y^2)+ (64x^6)(-27y^3)+(32x^5)(81y^4) + (16x^4)(-243y^5)+(8x^3)(729y^6) + (4x^2)(2187y^7)+ (2x)(6561y^8)+(-19683y^9))#
#=>color(green)((2x-3y)^9 = 512x^9−6912x^8y+41472x^7y^2−145152x^6y^3+326592x^5y^4−489888x^4y^5+489888x^3y^6−314928x^2y^7+118098xy^8−19683y^9)#
