Question

How do you expand `(2y-x^4)^6`?

Answer 1

`(2y-x^4)^6 = x^24 -12*y*x^20+ 60*y^2*x^16 - 160*y^3*x^12+ 240*y^4*x^8 - 192*y^5*x^4+ 64*y^6`

(may contain errors.)
edit: checked.

Explanation:

if you haven't learned the `(a+b)^n` theorem, then you can go the long way, by breaking it down to `(2y-x^4)^2*(2y-x^4)^2*(2y-x^4)^2`
and taking it peace by peace, if that what you were looking for comment and I'll try to write it.

or you can use the expansion theorem, learn more about it and it;s proofs here which most of them may seem scary but no worries you won't need to prove it to answer :)
(or jump to the section called Examples, it's what I'm doing.)

or the trick to the expansion theorem, (you can always prove it again by trying to expand `(x+y)^2 , (x+y)^3 ...` then you can try it with a negative sign....
If you do so, (I'm guessing you don't have time now) You will notice a pattern that I will use in my step by step answer.)

1) You have an equation of the 6th degree, so write down the product of the two terms seven times

`(2y-x^4)^6 = (2y)(x^4) + (2y)(x^4) + (2y)(x^4) + (2y)(x^4) + (2y)(x^4) + (2y)(x^4) + (2y)(x^4)`

2) Change the sign. Since we have a `-` in `(2y-x^4)^6` the sign will alter between each term starting from a `+` sign. (if it was positive then they all stay `+`'s )

`(2y-x^4)^6 = (2y)(x^4) + (2y)(x^4) - (2y)(x^4) + (2y)(x^4) - (2y)(x^4) + (2y)(x^4) - (2y)(x^4)`

3) Take the first term `(2y)` and power it up to zero, the second to one, and so on, until the last term becomes to the six

`(2y-x^4)^6 = (2y)^0(x^4) - (2y)^1(x^4) + (2y)^2(x^4) - (2y)^3(x^4) + (2y)^4(x^4) - (2y)^5(x^4) + (2y)^6(x^4)`

4) Take the other term `(x^4)` and power it up from zero to the six but from the end of the equation

`(2y-x^4)^6 = (2y)^0(x^4)^6 - (2y)^1(x^4)^5 + (2y)^2(x^4)^4 - (2y)^3(x^4)^3 + (2y)^4(x^4)^2 - (2y)^5(x^4)^1 + (2y)^6(x^4)^0`

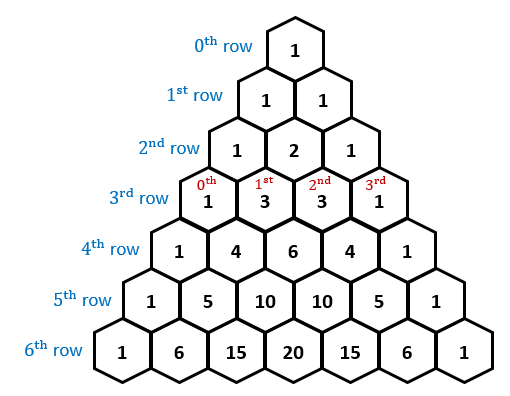
5) Add the coefficients. these can be found from the Pascal triangle.
since it is an expression of the sixth degree, count down the triangle from zero to six

They are `1, 6, 5, 20, 15, 6, 1`.

Add them in front of each term in order:
# (2y-x^4)^6 = 1(2y)^0(x^4)^6 -6 (2y)^1(x^4)^5+ 15(2y)^2(x^4)^4 - 20(2y)^3(x^4)^3+ 15(2y)^4(x^4)^2- 6 (2y)^5(x^4)^1+ 1(2y)^6(x^4)^0 #

6) Simplify.

`(2y-x^4)^6 = (x^4)^6 -6 (2y)(x^20)+ (15*4)(y^2)(x^16) - 20(8)(y)^3(x^12) + 15(16)(y)^4(x^8) - 6 (32)(y)^5(x^4) + (2y)^6`

(don't forget to power up the coefficient if in brakets)

`(2y-x^4)^6 = x^24 -12*y*x^20+ 60*y^2*x^16 - 160*y^3*x^12+ 240*y^4*x^8 - 192*y^5*x^4+ 64*y^6`