Question

How do you convert `0.18bar(3)` to a fraction?

Answer 1

`183/1000`

Explanation:

To convert a decimal to a fraction, you have to see how many places the decimal is. This chart may help: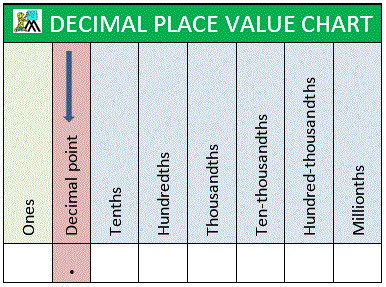

After you know what place the decimal ends at, you put the numbers after the decimal point over the place. For example, your decimal `0.1bar83` repeating ends in the thousandths place, so you would put `183` over `1000`. If you had `0.47`, you can see that it ends in the hundredths place, so you would put `47` over `100`.

If you were to have a full number with your decimal, it would stay a whole number in you fraction. For example, say I had `500.678`. I would write it as a decimal as `500 678/1000`, then you would put it in simplest form: `500 439/500`.

Your number is already in simplest form, but if you were to need to put a number in simplest form, you have to get the number to where the numerator and the denominator have no more common factors.

So: `1/3` is in simplest form because one and three have no common factors but,
`2/4` is not because two and four still share the factor of two.

I hope this makes sense. If you need more information on common factors and simplest form, go to

Common Factors

or

Simplest Form

Answer 2

`0.18bar(3) = 11/60`

Explanation:

Given:

`0.18bar(3)`

Multiply by `100(10-1)` to get an integer...

`100(10-1) 0.18bar(3) = 183.bar(3)-18.bar(3) = 165`

Divide both ends by `100(10-1)` and simplify...

`0.18bar(3) = 165/(100(10-1)) = (11*color(red)(cancel(color(black)(15))))/(60*color(red)(cancel(color(black)(15)))) = 11/60`

Why `100(10-1)` ?

The first multiplier `100` shifts the given number two places to the left, so the repeating portion starts just after the decimal point. The `10` multipler shifts it one further place to the left (the length of the repeating pattern), then the `-1` subtracts the original to cancel the repeating tail.