Question

Please use the picture and answer part a,b, and c. I need help in how to find the domain of each of the function and interval(s) where they are continuous?

Answer 1

Please see below.

Explanation:

.

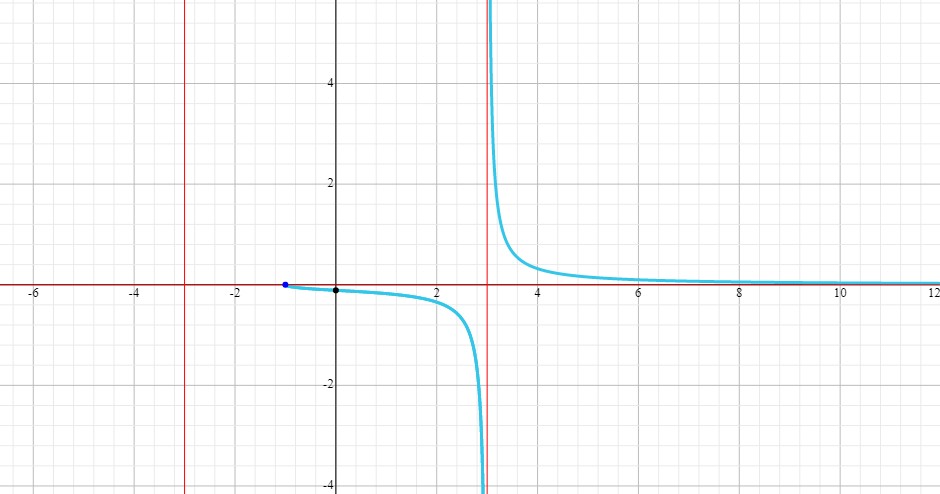
`a)`, `f(x)=(sqrt(x+1))/(x^2-9)`

Let's set it equal to zero to find the `x`-intercept:

`(sqrt(x+1))/(x^2-9)=0`

`sqrt(x+1)=0`

`x+1=0`

`x=-1`

We know that the graph intercepts the `x`-axis at `x=-1`. We also notice that for `x < -1`, we get a negative value under the radical and the graph will have the imaginary part of this function in that region. But we are only concerned with the real number domain. As such, `x > -1`.

Let's set the denominator equal to zero and solve for its roots:

`x^2-9=0`

`x=+-3`

This means that `x=3` and `x=-3` are vertical asymptotes because those values of `x` give us a `0` in the denominator and cause `y` to go to `oo`.

The domain of this function is:

`-1 < x < 3` and `3 < x < oo`

In each interval, the function is continuous. At `x=3`, it is discontinuous.

`x=-3` is an asymptote for the imaginary part. The real part of the function only has one vertical asymptote which is `x=3`.

Since the degree of the numerator is smaller than the degree of the denominator, `y=0` which is the `x`-axis is the horizontal asymptote. Here is the graph:

![enter image source here]
()

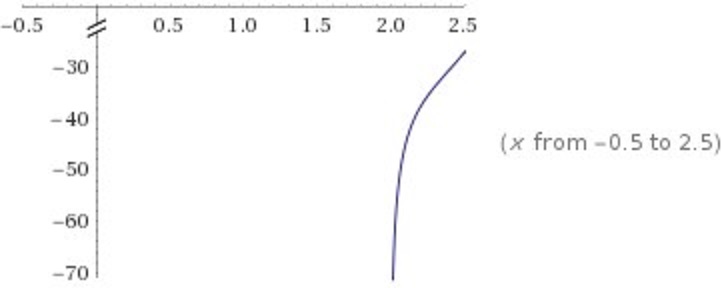
`b)`, `f(x)=x^4log(x-2)`

At `x=2`, we have `f)x)=2^4(log(0))`. `log(0)` is undefined and makes your function go to `-oo`. Therefore, `x=2` is a vertical asymptote.

At `x=3`, `f(x)=3^4(log(1))=3^4(0)` because `log(1)=0`. This means that at `x=3`, the graph crosses the `x`-axis.

The image below shows the graph of the function between `x=-0.5` and `x=2.5`:

![enter image source here]
()

The image below shows the graph of the function between `x=-3` and `x=15`:

The image below shows the graph of the function to the right of the vertical asymptote `x=2`

The domain of the function is:

`2 < x < oo` which is also the interval where the function is continuous.

`c)`, `f(x)=cosx` if `x <= 0` and `f(x)=3` if `x > 0`

Since this is a piece-wise function, it is discontinuous at `x=0`.

Its domain is:

`-oo < x <= 0` and `0 < x < oo`. At `x=0` there is a hole as shown in the graph below..

The function is continuous within each interval in the domain.

Here is the graph of the function: