Question

How do i solve this?

Answer 1

As X is equidistant (5m) from three vertices of the triangle `ABC`,X is the circumcentre of `DeltaABC`

So `angleBXC=2*angleBAC`

Now

`BC^2=XB^2+XC^2-2XB*XC*cosangleBXC`

`=>BC^2=5^2+5^2-2*5^2*cos/_BXC`

`=>BC^2=2*5^2(1-cos(2*/_ BAC)`

`=>BC^2=2*5^2*2sin^2 /_BAC`

`=>BC=10sin/_BAC=10sin80^@=9.84m`

Similarly

`AB=10sin/_ACB=10sin40^@=6.42m`

And

`AC=10sin/_ABC=10*sin60^@=8.66m`

Answer 2

`AB~~6.43m`
`BC~~9.89m`
`AC~~8.66m`

Explanation:

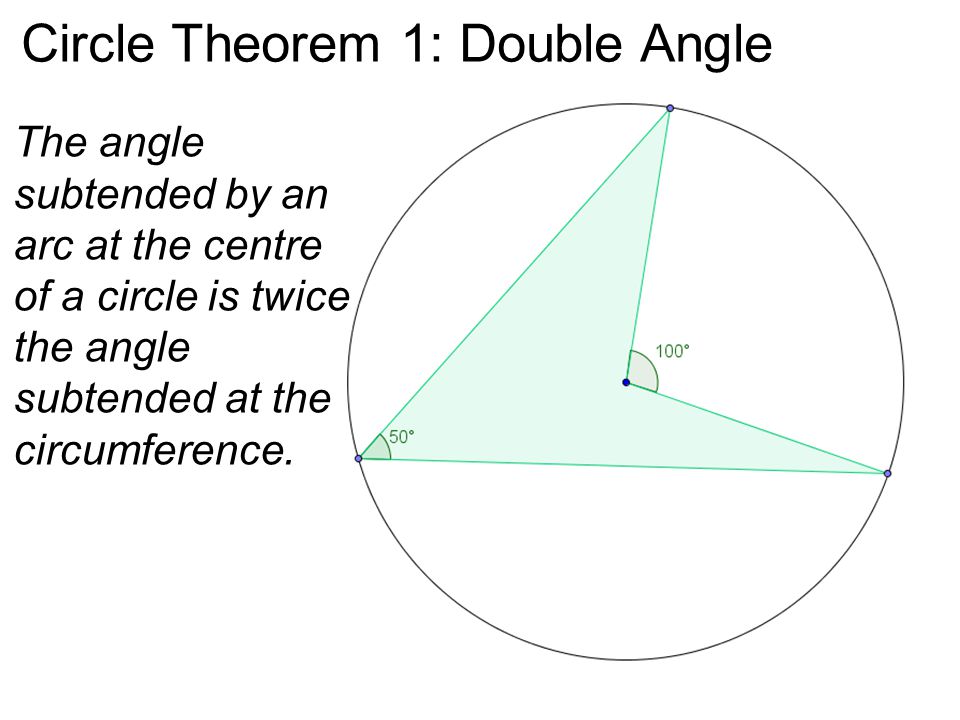
We can solve this using circle theorem:

We know that `XA=XB=XC=5m` therefore the three sides are all radii of a circle with a radius of `5m`

Therefore, we know:
`2/_BCA=/_BXA`
`2/_ABC=/_AXC`
`2/_BAC=/_BXC`

`/_BXC=2(80)=160`
`/_AXC=2(60)=120`
`/_BXA=2(40)=80`

Using the cosine we know that:
`c^2=a^2+b^2-2bacosC`
`c=sqrt(a^2+b^2-2bacosC)`

`AB=sqrt(AX^2+XB^2-2(AX)(XB)cos(/_AXB))`
`color(white)(AB)=sqrt(5^2+5^2-2(5^2)cos(80))`
`color(white)(AB)~~6.43m`

`BC=sqrt(BX^2+XC^2-2(BX)(XC)cos(/_BXC))`
`color(white)(BC)=sqrt(5^2+5^2-2(5^2)cos(160))`
`color(white)(BC)~~9.89m`

`AC=sqrt(AX^2+XC^2-2(AX)(XC)cos(/_AXC))`
`color(white)(AC)=sqrt(5^2+5^2-2(5^2)cos(120))`
`color(white)(AC)~~8.66m`

Sides:
`AB~~6.43m`
`BC~~9.89m`
`AC~~8.66m`