Question

Question #ac026

Answer 1

`sin(2theta+pi/3)=1/2`

`=>sin(2theta+pi/3)=sin(pi/6)`

`=>2theta+pi/3=pi/6`

`=>2theta=-pi/6`
`=>theta=-pi/12" not in the given range"`

Again

`sin(2theta+pi/3)=1/2=sin(pi-pi/6)`

`=>2theta+pi/3=(5pi)/6`

`=>2theta=(5pi)/6-pi/3`

`=>2theta=(3pi)/6=pi/2`,

`=>theta=pi/4`

Again

`sin(2theta+pi/3)=1/2=sin(2pi+pi/6)`

`=>2theta+pi/3=(13pi)/6`

`=>2theta=(13pi)/6-(2pi)/6`

`=>2theta=(11pi)/6`

`=>theta=(11pi)/12`

So for `0<=theta<=pi` the solutions are

`theta =pi/4 and theta =(11pi)/12`

Answer 2

Due to the request for clarification in the question, this answer is a bit long. Feel free to skip over any unneeded explanations.

---

Unless otherwise specified, we generally consider the argument of a trigonometric function to be in radians. Radians are, in a sense, the natural way of measuring an angle within a circle, as they relate the radius of the circle to the angle measured (one radian is the measure of an angle subtended by an arc whose length equals the radius). A full circle is `2pi` radians (equivalent to `360^@`), and as such, `pi` appears quite commonly in well known angles.

---

With that in mind, let's see what this problem is asking.


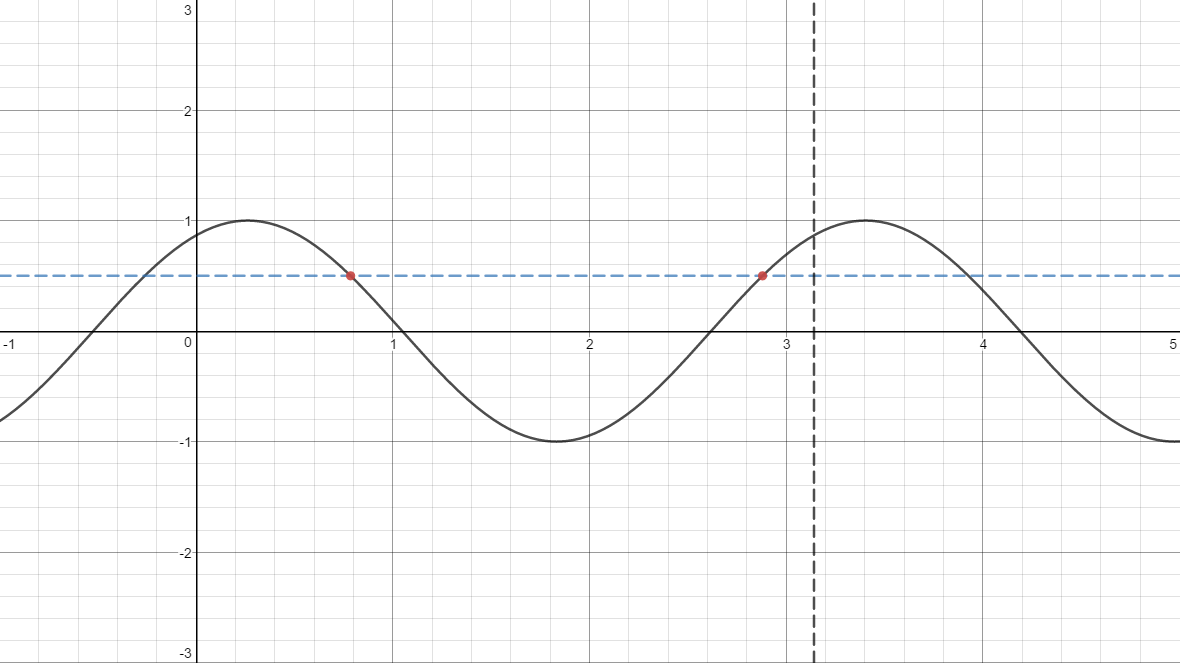
The above is a graph of `y = sin(2x+pi/3)`, with dashed lines showing `y=1/2` and `x=pi`. Note that between `x=0` and `x=pi`, the `y=1/2` line intersects our graph at two points. The `x`-coordinates of those points are our solutions.

To figure out what those points are, we will consult the unit circle .

On the unit circle, the `x` and `y` coordinates tell us the value of `cos(theta)` and `sin(theta)`, respectively. For example, from the circle, we see that `sin(theta) = 1/2` at `theta = pi/6` and `theta = (5pi)/6`.

(The angles shown on the circle and the values of sine and cosine at those angles are good to have memorized. As a side note, they can be derived by using the sohcahtoa definition on the special right triangles with angles `30^@-60^@-90^@` or `45^@-45^@-90^@`. Additionally, because it is a circle, we can add or subtract any multiple of `2pi` (`360^@`) to an angle without changing the values of the trig functions.)

From the above, we now know that for `sin(x)` to equal `1/2`, we need `x = pi/6 + 2pik` or `x = (5pi)/6+2pik` where `k` is an integer. We can now solve the problem algebraically. Substituting our argument `2theta+pi/3` for `x`, we get

`2theta+pi/3 = pi/6 + 2pik`

`=> 2theta = -pi/6+2pik`

`=> theta = -pi/12 + pik`

OR

`2theta+pi/3 = (5pi)/6+2pik`

`=> 2theta = pi/2 + 2pik`

`=> theta = pi/4+pik`

Now we consider the restriction `0 <= theta <= pi` to see what integers we can use for `k`. To get `theta` to stay within that range, we must have `k=1` for the first possibility, and `k = 0` for the second. Thus, we get two answers:

`theta = -pi/12 + 1pi = (11pi)/12`
OR
`theta = pi/4 + 0pi = pi/4`

Thus, we have the solution set `theta in {pi/4, (11pi)/12}`.

Checking, we find that the equality hold for each of the above values:

`sin(2(pi/4)+pi/3) = sin(pi/2+pi/3) = sin((5pi)/6) = 1/2`

`sin(2((11pi)/12)+pi/3) = sin((11pi)/6+pi/3) = sin(pi/6+2pi) = 1/2`