Question #f4fb1
1 Answer
Feb 9, 2017
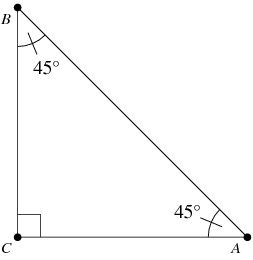
Let us consider a right angled isosceles triangle ABC inwhich
So by Pythgorean theorem
Again
So

Let us consider a right angled isosceles triangle ABC inwhich
So by Pythgorean theorem
Again
So

