How do you find the density of a cone of radius "5 cm"5 cm and height "2 cm"2 cm if its mass is equal to "6 g"6 g and its volume is equal to "52.36 cm"^352.36 cm3 ?

1 Answer
Stefan V.
Sep 6, 2017

Here's what I got.

Explanation:

Start by calculating the volume of the cone.

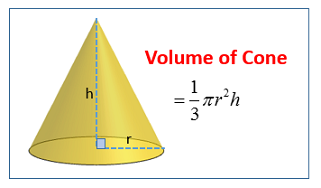
![http://www.onlinemathlearning.com/http://volume-cone.html](https://useruploads.socratic.org/Rd6gpkWJQzVqBIMUOOuy_xvolume-of-cone.png.pagespeed.ic.2-YhHAnIvd.png)

In your case, you have

  • r = "5 cm" ->r=5 cm→ the radius of the cone
  • h = "2 cm" ->h=2 cm→ the height of the cone

Plug your values into the equation to get

V = 1/3 * pi * "5 cm"^2 * "2 cm"V=13⋅π⋅5 cm2⋅2 cm

V = "52.36 cm"^3V=52.36 cm3

Now, to find the density of the material, you must determine the mass of exactly "1 cm"^31 cm3 of material. To do that, use the fact that "52.36 cm"^352.36 cm3 of material have a mass of "6 g"6 g

1 color(red)(cancel(color(black)("cm"^3))) * "6 g"/(52.36 color(red)(cancel(color(black)("cm"^3)))) = "0.1146 g"

Since this represents the mass of exactly "1 cm"^3 of this material, you can say that

color(darkgreen)(ul(color(black)("density = 0.1 g cm"^(-3)))

The answer is rounded to one significant figure.

SIDE NOTE This is a very low value for the density of a material, so make sure to double-check the values given to you for the mass of the cone and for its dimensions.

Related questions
See all questions in Density
Impact of this question
11060 views around the world
You can reuse this answer
Creative Commons License