A typical heating curve of water is shown below.
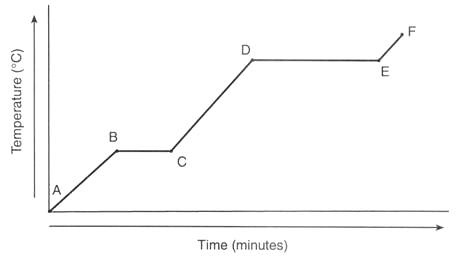
There are three separate heat transfers involved in this problem:
- #q_1# = heat required to warm the ice from -25 °C to 0 °C (Point A to B in the diagram)
- #q_2# = heat required to melt the ice to water at 0 °C (Point B to C)
- #q_3# = heat required to warm the water from 0 °C to 70. °C (From Point C part way to Point D)
#q = q_1 + q_2 + q_3 = mc_1ΔT_1 + mΔ_text(fus)H + mc_3ΔT_3#
where
#q_1, q_2,# and #q_3# are the heats involved in each step
#m# is the mass of the sample
#ΔTcolor(white)(m) = T_"f" -T_"i"#
#c_1color(white)(mm) = "the specific heat capacity of ice" = "2.03 J·°C"^"-1""g"^"-1"#
#c_3color(white)(mm) = "the specific heat capacity of water" = "4.179 J·°C"^"-1""g"^"-1"#
#Δ_text(fus)H = "the enthalpy of fusion of ice" = 3.33 × 10^5 color(white)(l)"J·kg"^"-1"#
#bbq_1#
#ΔT_1 = "0 °C - (-25 °C)" = "25 °C"#
#q_1 = mc_1ΔT_1 = 2.0 × 10^3 color(red)(cancel(color(black)("g"))) × 2.03 color(white)(l)"J"·color(red)(cancel(color(black)( "°C"^"-1""g"^"-1"))) × 25 color(red)(cancel(color(black)("°C"))) = 1.02 × 10^5color(white)(l) "J"#
#bbq_2#
#q_2 = 2.0 color(red)(cancel(color(black)("kg"))) × 3.33 × 10^5color(white)(l) "J"·color(red)(cancel(color(black)("kg"^"-1"))) = 6.66 × 10^5color(white)(l) "J"#
#bbq_3#
#ΔT = "70. °C - 0 °C" = "70. °C"#
#q_3 = mcΔT = 2.0 × 10^3 color(red)(cancel(color(black)("g"))) × 4.179 color(white)(l)"J"·color(red)(cancel(color(black)( "°C"^"-1""g"^"-1"))) × 70. color(red)(cancel(color(black)("°C"))) = 5.85 × 10^5color(white)(l) "J"#
#q = q_1 + q_2 + q_3 = (1.02 + 6.66 + 5.85) × 10^5color(white)(l) "J" = 14.0 × 10^5color(white)(l) "J"#
#= 1.40 × 10^6color(white)(l) "J"#
The process absorbs #1.40 × 10^6color(white)(l) "J"# of heat.



