The first thing to do is get rid of the arctan. We can do this by realizing that as #x -> oo#, #arctan(x)->pi/2#. We can see this from the graph (or just by knowing that tan(x) has horizontal asymptotes at #x=pi/2#):
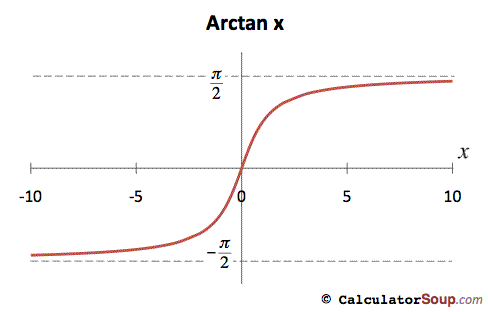
This means that #arctan(x)# on #[0,oo) <= pi/2# and therefore
#int_0^oo arctan(x)/(2+e^x)dx<= pi/2 int_0^oo 1/(2+e^x)dx#
This is still a bit tricky to integrate, so we can simplify further:
#2+e^x > e^x# which means
#1/(2+e^x)<1/e^x# so,
#pi/2 int_0^oo 1/(2+e^x)dx <= pi/2 int_0^oo 1/(e^x)dx#
Now we have:
#int_0^oo arctan(x)/(2+e^x)dx <= pi/2 int_0^oo 1/(e^x)dx#
and # pi/2 int_0^oo 1/(e^x)dx# is something we can integrate!
#pi/2 int_0^oo 1/(e^x)dx = lim_(t->oo) pi/2 int_0^t e^-x dx#
#=lim_(t->oo) pi/2[-e^-x]_0^t#
# = lim_(t->oo) pi/2[-e^-t-(-e^0)]#
#= pi/2[0+1]#
#=pi/2# so
#int_0^oo arctan(x)/(2+e^x)dx <= pi/2#
and therefore it is convergent :)


