Question

How do you evaluate the integral of `x^2` from 1 to 2?

Answer 1

`7/3`

Explanation:

Here, we have `f(x)=x^2`.

If `f` is continuous on `[a,b]` and `f(x)=F'(x)`, then

`int_a^bf(x)dx=F(b)-F(a)`

So, when we have

`int_1^2x^2dx`

we must find the antiderivative of the function `x^2` using the rule:

`intx^ndx=x^(n+1)/(n+1)+C`

Using this rule, we see that `F(x)` is `x^3/3`.

Thus,

`int_1^2x^2dx=F(2)-F(1)`

Note that `F(2)-F(1)=[x^3/3]_1^2`, this is just another way of writing it.

`F(2)-F(1)=2^3/3-1^3/3=8/3-1/3=7/3`

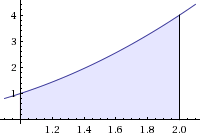
This means that the area between the `x^2` and the `x`-axis on the interval `[1,2]` is `"7/3"`.