Question

How do you find horizontal asymptotes for `f(x) = arctan(x)` ?

Answer 1

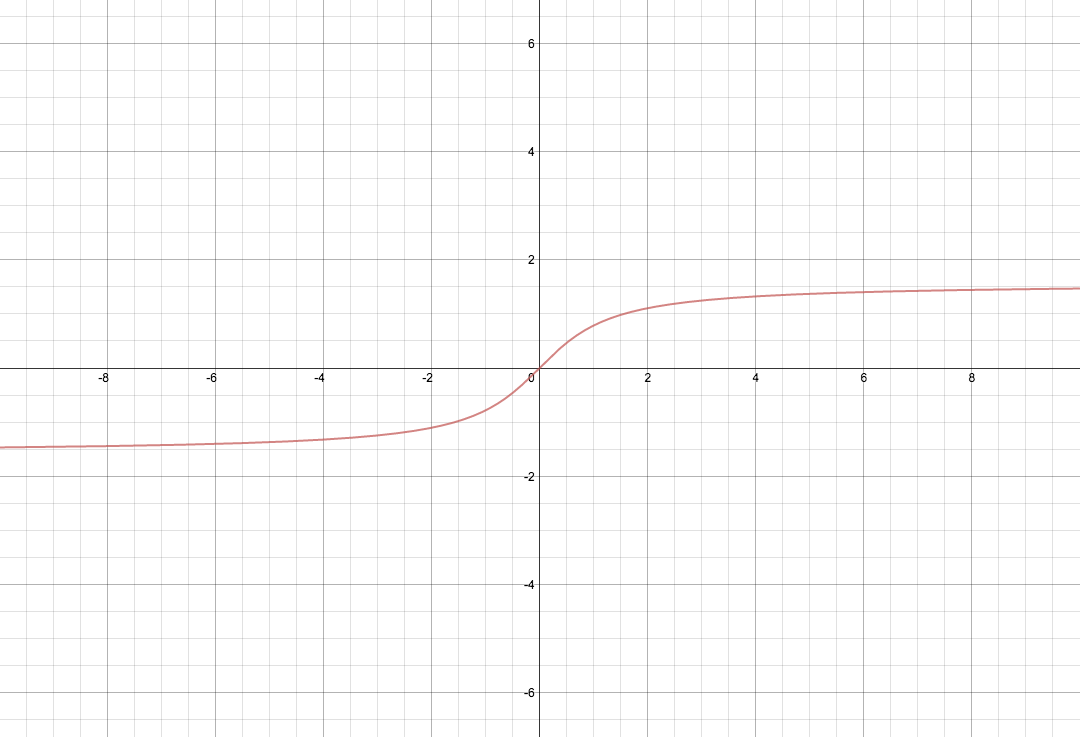
By definition, `arctan x` is the inverse function of the restriction of the tangent function `tan` to the interval `(-pi/2,pi/2)` (see inverse cosine and inverse tangent ).

The tangent function has vertical asymptotes `x=-pi/2` and `x=pi/2`, for `tan x=sin x/cos x` and `cos \pm pi/2=0`.

Moreover, the graph of the inverse function `f^(-1)` of a one-to-one function `f` is obtained from the graph of `f` by reflection about the line `y=x` (see finding inverse functions ), which transforms vertical lines into horizontal lines.

Thus, the vertical asymptotes `x=\pm pi/2` for `y=tan x` correspond in this reflection to the horizontal asymptotes `y=\pm pi/2` for `y=arctan x`.

Here's a graph of arctan(x):