Question

How do you graph the equations `(x - 2)^2 + (y + 2)^2 = 8` and `r = 4 \cos \theta - 4 \sin \theta`?

Answer 1

This two equations give birth to the same graph: a circumference centered in `C=(2,-2)` with radius `r=2 sqrt{2}`.

The equation `(x-2)^2+(y+2)^2=8` is the result of a scaling by a factor of `2 sqrt{2}` and the a translation of vector `vec v = (2,-2)`, applied in this order to a unit circle `x^2+y^2=1`.
In fact, the scaling equations are
`(x"'",y"'")=2 sqrt{2} (x,y)=(2 sqrt{2} x, 2 sqrt{2} y)`
and the translation equations are
`(x"''",y"''")=(x"'"+2,y"'"-2)`

To find out that the result of this transformation is the equation `(x"''"-2)^2+(y"''"+2)^2=8`, we have to invert these transformations. So we have the inverse translation `(x"'",y"'")=(x"''"-2,y"''"+2)` and the inverse scaling `(x,y) = 1/{2 sqrt{2}} (x"'",y"'")`.
Now we can compose them, getting `(x,y) = 1/{2 sqrt{2}} (x"'",y"'") = 1/{2 sqrt{2}} (x"''"-2,y"''"+2)=({x"''"-2}/{2 sqrt{2}},{y"''"+2}/{2 sqrt{2}})`.
We can substitute these into the unit circle equation, getting
`({x"''"-2}/{2 sqrt{2}})^2+({y"''"+2}/{2 sqrt{2}})^2=1`
`(x"''"-2)^2/8+(y"''"+2)^2/8=1`
`(x"''"-2)^2+(y"''"+2)^2=8`

This shows that the first equation is a circle of center `C=(2,-2)` and radius `r=2 sqrt(2)`.

To show that the polar equation `r=4 cos theta - 4 sin theta` gives the same graph, we simply convert polar coordinates to cartesian coordinates (`r=sqrt{x^2+y^2}` and `theta=arctan(y/x)`) to show that this is the polar form of the equation `(x-2)^2+(y+2)^2=8`. If we substitute `r` and `theta` in the polar equation, we get:
`sqrt{x^2+y^2}=4 cos(arctan(y/x)) - 4 sin(arctan(y/x))`.

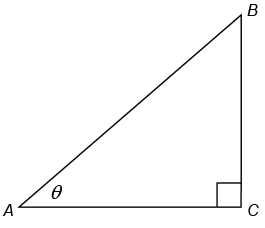
Now consider a right triangle with the two legs `bar{AC}=x` and `bar{BC}=y`, so `bar{AB}=sqrt{x^2+y^2}`.
![http://www.skwirk.com/p-c_s-12_u-95_t-229_c-764/sine/nsw/sine/trigonometry/elements]()
`sin theta = bar{BC}/bar{AB}=y/sqrt{x^2+y^2}`
`cos theta = bar{AC}/bar{AB}=x/sqrt{x^2+y^2}`
`tan theta = y/x rArr theta = arctan(y/x)`
So we get
`y/sqrt{x^2+y^2}=sin theta = sin (arctan(y/x))`
`x/sqrt{x^2+y^2}=costheta = cos(arctan(y/x))`
And these equalities are valid for non-negative values of `x` and `y` because of the symmetry properties of the functions sine, cosine and arctangent.

So we can rewrite the cartesian equation that we got from the polar one, getting:
`sqrt{x^2+y^2}=4 x/sqrt{x^2+y^2} - 4 y/sqrt{x^2+y^2}`
`x^2+y^2=4 x- 4 y`
`x^2-4x+y^2+ 4 y=0`
Finally, we complete the squares:
`x^2-4x+4+y^2+ 4 y+4=4+4`
`(x-2)^2+(y+2)^2=8`