Question

How do you solve `cosxtanx=1/2`?

Answer 1

`pi/6, (5pi)/6`

Explanation:

`cos x.tan x = 1/2`
`cos x(sin x)/(cos x) = 1/2`
Divide by cos x, under condition `=>` cos x diff. to zero,
or x diff. to `pi/2, (3pi)/2`
`sin x = 1/2`
Use trig table of special arcs and unit circle `=>`
`sin x = 1/2` `=>` arc `x = pi/6` , and arc `x = (5pi)/6`
General answers:
`x = pi/6 + 2kpi`
`x = (5pi)/6 + 2kpi`

Answer 2

`x = 30^@` or `pi/6` and `150^@` or `(5pi)/6`

Explanation:

Using the trigonometric identity, `color(red)(tan x) = color(green)(sin x)/color(blue)(cos x)`,

this question can be written as `color(blue)(cosx)* color(green)(sin x)/color(blue)(cos x) = 1/2`

`color(white)("XXXXXXXXXXXXXXXX")color(blue)cancel(cosx)* color(green)(sin x)/color(blue)cancel(cos x) = 1/2`

`color(white)("XXXXXXXXXXXXXXXX")color(green)sinx = 1/2`


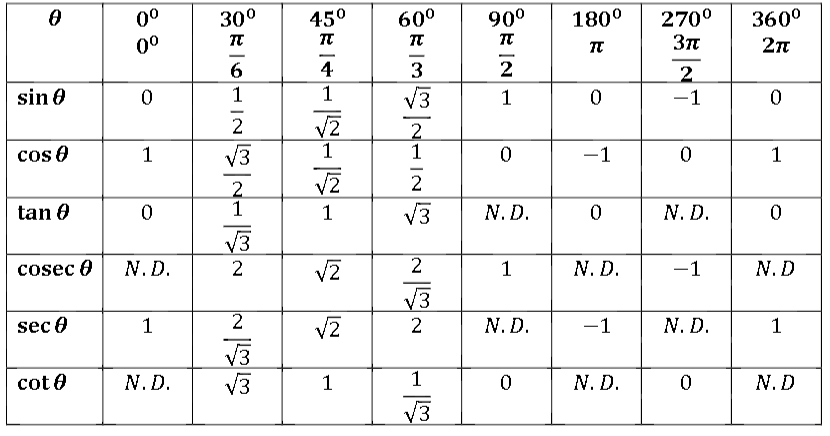
Note: 'N.D.' means Not Defined. For example, `a/0` is not defined, where `a` is any non-zero number like 1, 4, 647 etc. But, `0/a = 0`.

As you can see in this table, we get the value of `x` as `30^@` or `pi/6`.
![https://socratic.org/questions/how-do-you-find-the-exact-functional-value-sin-195-using-the-cosine-sum-or-diffe]()
This is called a 'Unit Circle'.

The values in brackets are (`cos`,`sin`).
`sin` is positive in the first and second quadrants. Since we need `+ 1/2`, we consider these quadrants only.

`30^@` is the value of `x` in the first quadrant.
To get the second value of `x`(in second quadrant), we subtract `pi/6` from `pi`.
`pi - pi/6 = (6pi)/6 - pi/6 = (5pi)/6 or 150^@`.

Also note, here `pi` is `pi` radians, which is equal to `180^@`.
Check out this video for more understanding:
Intro to Arcsin