How do you solve $\frac{6 y}{2 y + 6} + \frac{y + 18}{3 y + 9} = \frac{7 y + 17}{y + 3}$ $\frac { 6y } { 2y + 6} + \frac { y + 18} { 3y + 9} = \frac { 7y + 17} { y + 3}$ ?

Question

How do you solve $\frac{6 y}{2 y + 6} + \frac{y + 18}{3 y + 9} = \frac{7 y + 17}{y + 3}$ $\frac { 6y } { 2y + 6} + \frac { y + 18} { 3y + 9} = \frac { 7y + 17} { y + 3}$ ?

1 Answer

Impact of this question

2793 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-04-19T22:16:52

No real solution. Read the explanation carefully.

Explanation:

$\frac{6 y}{2 y + 6} + \frac{y + 18}{3 y + 9} = \frac{7 y + 17}{y + 3}$ $(6y)/(2y+6)+(y+18)/(3y+9)=(7y+17)/(y+3)$

We can rewrite it as:-

$\frac{6 y}{2 (y + 3)} + \frac{y + 18}{3 (y + 3)} = \frac{7 y + 17}{y + 3}$ $(6y)/[2(y+3)]+(y+18)/[3(y+3)]=(7y+17)/(y+3)$

$\Rightarrow \frac{9 y + y + 18}{3 (y + 3)} = \frac{7 y + 17}{y + 3}$ $=>(9y+y+18)/(3(y+3))=(7y+17)/(y+3)$

Cross multiply;

$\Rightarrow (10 y + 18) (y + 3) = 3 (7 y + 17) (y + 3)$ $=>(10y+18)(y+3) = 3(7y+17) (y+3)$

$\Rightarrow (10 y + 18) (y + 3) - 3 (7 y + 17) (y + 3) = 0$ $=>(10y+18)(y+3)-3(7y+17) (y+3)=0$

Taking $(y + 3)$ $(y+3)$ common;

$\Rightarrow (y + 3) (10 y + 18 - 21 y - 51) = 0$ $=>(y+3)(10y+18-21y-51)=0$

$\Rightarrow (y + 3) (- 11 y - 33) = 0$ $=>(y+3)(-11y-33)=0$

$\Rightarrow - 11 \cdot (y + 3) \cdot (y + 3) = 0$ $=>-11*(y+3)*(y+3)=0$

$\Rightarrow {(y + 3)}^{2} = 0$ $=> (y+3)^2=0$

$\Rightarrow y + 3 = 0$ $=> y+3 = 0$ $\Rightarrow y = - 3$ $=> color(red)(y=-3)$

BUT there is a catch.

We might think that $y = - 3$ $y=-3$ is the solution but try to substitute this value back into the original equation i.e.

$\frac{6 y}{2 y + 6} + \frac{y + 18}{3 y + 9} = \frac{7 y + 17}{y + 3}$ $(6y)/(2y+6)+(y+18)/(3y+9)=(7y+17)/(y+3)$

We find that terms in the denominator become zero.
$2 \cdot (- 3) + 6 = - 6 + 6 = 0$ $2*(-3)+6 = -6+6=0$ ,
$3 \cdot (- 3) + 9 = - 9 + 9 = 0$ $3*(-3)+9=-9+9=0$ ,
$- 3 + 3 = 0$ $-3+3 = 0$ .

That means the expressions $\frac{6 y}{2 y + 6}, \frac{y + 18}{3 y + 9}, \frac{7 y + 17}{y + 3}$ $(6y)/(2y+6), (y+18)/(3y+9), (7y+17)/(y+3)$ become undefined ** at $y = - 3$ $y=-3$ since division by zero is not defined. Hence we cannot say for sure whether the left-hand-side equals the right-hand-side or not. So $y = - 3$ $y=-3$ is not a solution** to this equation.

Where did we go wrong?

Remember the step where we cross multiplied $y + 3$ $y+3$ . Cross multiplication, or in fact any kind of multiplication on both sides of the equation is allowed only when the number(s) being multiplied is/are non-zero. Therefore cross multiplication in that step is only valid if $y + 3 \neq 0$ $y+3!=0$ or $y \neq - 3$ $y!=-3$ . I.e. we are cross multiplying on the assumption that $y = - 3$ $y=-3$ is not a solution and even if it turns out to be a solution after solving the subsequent equations, we are going to neglect it.

$therefore$ we neglect $y=-3$ and hence, the given equation has no real solution.

Just to be sure, I checked on wolfram.
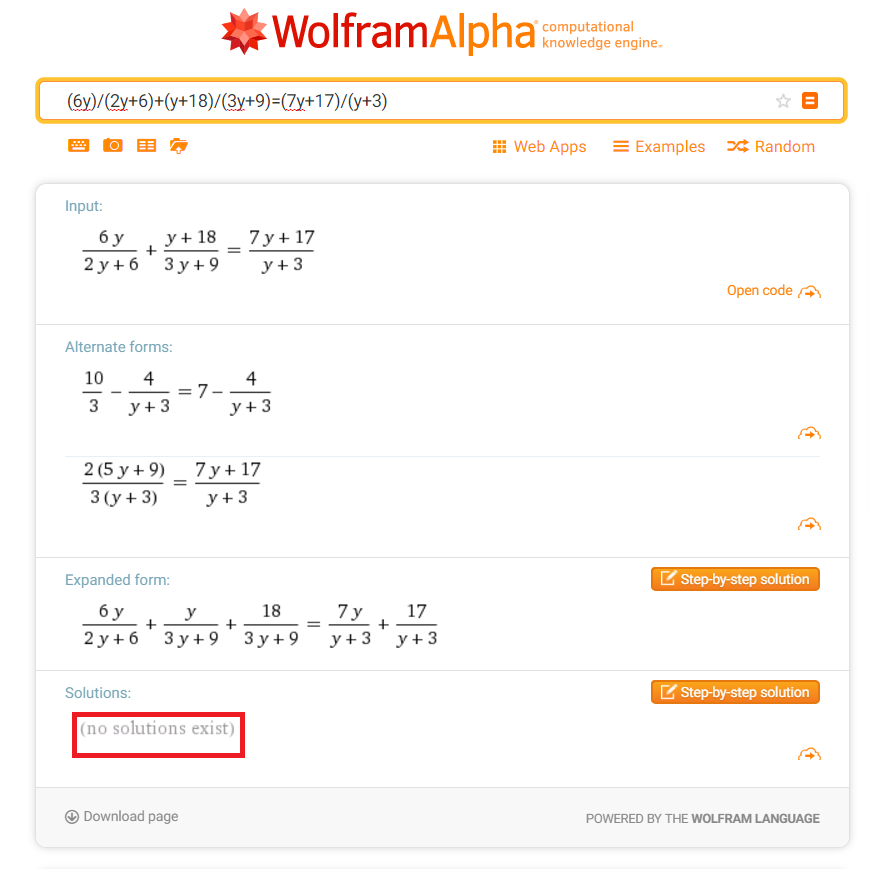![wolframalpha.com]( useruploads.socratic.org )

Science

Math

Humanities

... and beyond

How do you solve $\frac{6 y}{2 y + 6} + \frac{y + 18}{3 y + 9} = \frac{7 y + 17}{y + 3}$ $\frac { 6y } { 2y + 6} + \frac { y + 18} { 3y + 9} = \frac { 7y + 17} { y + 3}$ ?

1 Answer

Explanation:

Related questions

Impact of this question

Science

Math

Humanities

... and beyond

How do you solve \frac { 6y } { 2y + 6} + \frac { y + 18} { 3y + 9} = \frac { 7y + 17} { y + 3}6y2y+6+y+183y+9=7y+17y+3\frac { 6y } { 2y + 6} + \frac { y + 18} { 3y + 9} = \frac { 7y + 17} { y + 3}?

1 Answer

Explanation:

Related questions

Impact of this question

How do you solve $\frac{6 y}{2 y + 6} + \frac{y + 18}{3 y + 9} = \frac{7 y + 17}{y + 3}$ $\frac { 6y } { 2y + 6} + \frac { y + 18} { 3y + 9} = \frac { 7y + 17} { y + 3}$ ?