Question

How to find the moment of inertia of a solid cylinder about transverse (perpendicular) axis passing through its center?

The solution is of one line -
`I = (MR^2)/4 + (ML^2)/12`
I didn't understand how `(ML^2)/12` comes into play...

Answer 1

It needs to be done in three steps.
1. Stating Moment of Inertia of a infinitesimally thin Disk.
2. Application of Perpendicular Axis and Parallel axis Theorems.
3. Integrating over the length of the cylinder.
But first of all let's state the problem.

Explanation:

Figure 1.

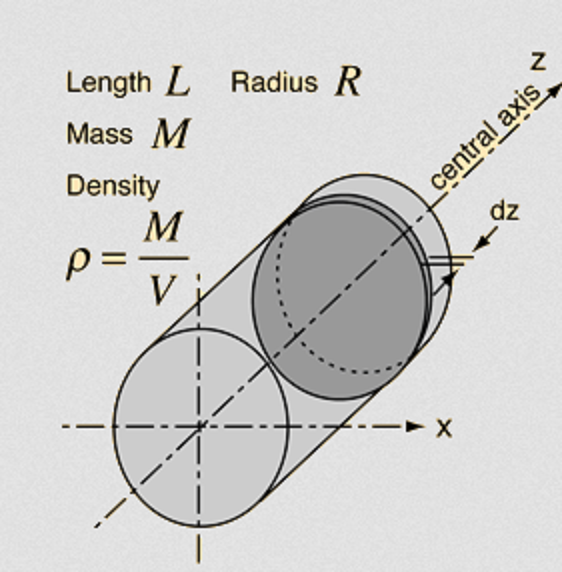
Let us consider a cylinder of length `L`, Mass `M`, and Radius `R` placed so that `z` axis is along its central axis as in the figure.
We know that its density `rho="Mass"/"Volume"=M/V`.

Figure 2.

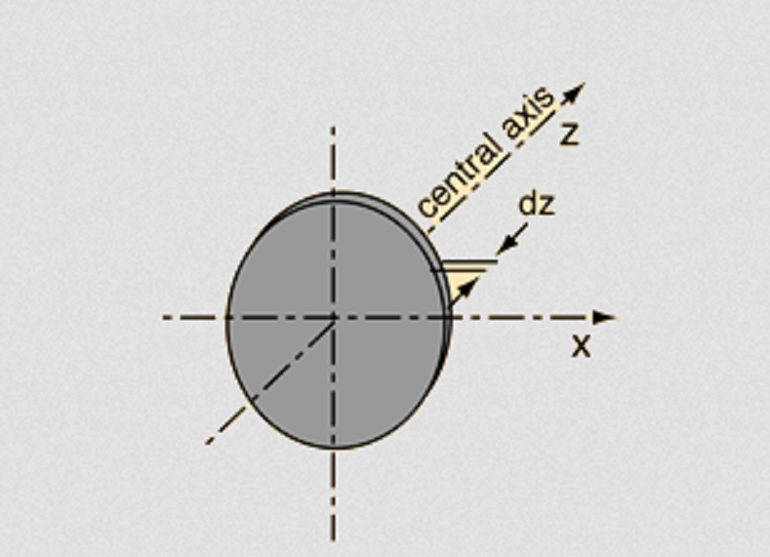
Let us consider that the cylinder is made up of infinitesimally thin disks each of thickness `dz`. If `dm` is the mass of one such disk, then
`dm=rho times "Volume of disk"`
or `dm=M/V times (pi R^2.dz)`,
since `V="Areal of circular face"xx"length"=pi R^2L`, we obtain
`dm=M/(pi R^2L) times (pi R^2.dz)`
or `dm=M/Ldz` ......(1)
Step 1.

We know that moment of inertia of a circular disk of mass `m` and of radius `R` about its central axis is is same as for a cylinder of mass `M` and radius `R` and is given by the equation
`I_z=1/2mR^2`. In our case

`dI_z=1/2dmR^2`......(2)
Step 2.

Observe from figure 2, that this moment of inertia has been calculated about `z` axis. In the problem we are required to find moment of inertia about transverse (perpendicular) axis passing through its center. Knowing that the desired axis of rotation is transverse, therefore we need to apply perpendicular axis theorem which states:

The moment of inertia about an axis which is perpendicular to the plane contained by the remaining two axes is the sum of the moments of inertia about these two perpendicular axes, through the same point in the plane of the object.
It follows that
`dI_z=dI_x+dI_y` .....(3)
Also from symmetry we see that moment of inertia about `x` axis must be same as moment of inertia about `y` axis.
`:. dI_x=dI_y` ......(4)
Combining the equations (3) and (4) we obtain
`dI_x=(dI_z)/2`, Substituting `I_z` from (2), we get
`dI_x=1/2xx1/2dmR^2`
or `dI_x=1/4dmR^2`

Let the infinitesimal disk be located at a distance `z` from the origin which coincides with the center of mass.

Now we make use of the parallel axis theorem about the `x` axis which states:

The moment of inertia about any axis parallel to that axis through the center of mass is given by

`I_"Parallel axis"=I_"Center of Mass"+"Mass"times"d^2`
where `d` is distance of parallel axis from Center of mass.
`dI_x=1/4dmR^2+dmz^2` ......(5)
Step 3.
Insert the value of `dm` calculated in (1) in moment of inertia equation (5) to express it in terms of `z` then integrate over the length of the cylinder from the value of `z=-L/2` to `z=+L/2`
`I_x=int_(-L/2)^(+L/2)dI_x=int_(-L/2)^(+L/2)1/4M/LdzR^2+int_(-L/2)^(+L/2)z^2 M/Ldz`
`I_x=1/4M/LR^2z+M/L z^3/3]_(-L/2)^(+L/2)`,
ignoring constant of integration because of it being definite integral.

`I_x=1/4M/LR^2[L/2-(-L/2)]+M/(3L) [(L/2)^3-(-L/2)^3]`
or `I_x=1/4M/LR^2L+M/(3L) (2L^3)/2^3`
or `I_x=1/4MR^2+1/12M L^2`