Question

Phosphorus-32 has a half-life of 14.0 days. Starting with 6.00 g of `""^32P`, how many grams will remain after 56.0 days?

Express the answer in numerically in grams.

Answer 1

`"Well what is a half of a half of a half of a half?"`

Explanation:

And `56*"days"` is FOUR half-lives....and so we got `1/2xx1/2xx1/2xx1/2=1/2^4=1/16` of the original mass of `""^32P`...

And given that the initial quantity was `6.00*g`...we are left with `6.00*gxx1/16=??*g`....

Answer 2

The mass remaining is `=0.375g`

Explanation:

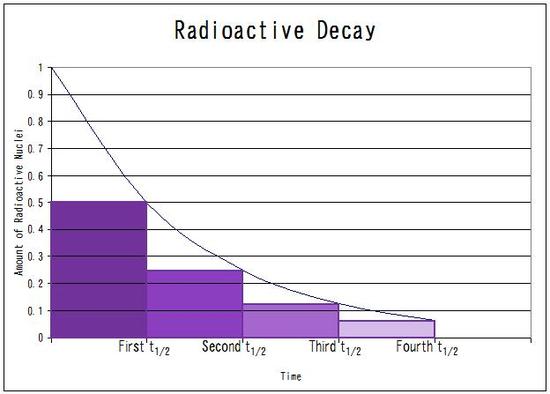
The half life is `t_(1/2)=14 "days"`

The number of half life of `" Phosphorus- 32 "` in `56` days is

`=t/t_(1/2)=56/14= 4 " half life "`

The initial mass of `" Phosphorus- 32 "` is `m_0=6.00g`

After each half life, the mass will decrease by `xx1/2`

Therefore,

the mass remaining is `=6/16=3/8=0.375g`