The acceleration-time graph of a particle moving in a straight line is as shown in figure. The velocity of the particle at time t = 0 is 2 m/s. The velocity after 2 seconds will be ?
(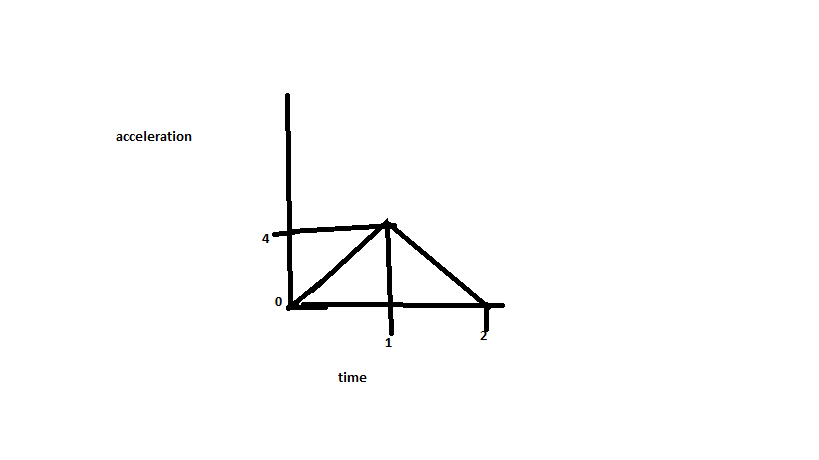 )
)
options :-
(1) 6 m/s
(2) 4 m/s
(3) 2 m/s
(4) 8 m/s
please answer with full explanation
note: all lines in the graph are straight
( )
)
options :-
(1) 6 m/s
(2) 4 m/s
(3) 2 m/s
(4) 8 m/s
please answer with full explanation
note: all lines in the graph are straight
1 Answer
I got
(1)
Explanation:
From Graph:
and
- from
#t=0# to#t=1\ s#
#dota=4\ ms^-3#
Integrating both sides with time we get#int\ dota\ dt=int\ 4\ dt#
#=>a=4t+C#
where#C# is a constant of integration to be calculated from initial conditions.
From Graph at#t=0# ,#a=0#
#:.a=4t\ ms^-2# ........(1)
Rewriting this as
#a=dotv=4t\ ms^-2#
Integrating both sides with time we get
#int\ dotv\ dt=int\ 4t\ dt#
#=>v=4t^2/2+C_1#
#=>v=2t^2+C_1#
where#C_1# is a constant of integration to be calculated from initial conditions. Given, at#t=0# #v=2\ ms^-1# . Inserting these values in above expression we get
#=>2=2(0)^2+C_1#
#=>C_1=2#
This gives us the expression for velocity as
#v=2+2t^2# .......(2)
and#v_(t=1)=4\ ms^-1# ...........(3) - from
#t=1# to#t=2\ s#
#dota=-4\ ms^-3#
Integrating both sides with time we get#int\ dota\ dt=int\ -4\ dt#
#=>a=-4t+C_2#
where#C_2# is a constant of integration to be calculated from initial conditions at#t=1\ s# .
From Graph at#t=1# ,#a=4\ ms^-2# . Inserting in above expression we get
#4=-4xx1+C_2#
#=>C_2=8#
#:.a=-4t+8\ ms^-2# ........(4)
Rewriting this as
#a=dotv=-4t+8\ ms^-2#
Integrating both sides with time we get
#int\ dotv\ dt=int\ (-4t+8)\ dt#
#=>v=-4t^2/2+8t+C_3#
#=>v=-2t^2+8t+C_3#
where#C_3# is a constant of integration to be calculated from calculated initial conditions at#t=1# #v=4\ ms^-1# . Inserting these values in above expression we get
#=>4=-2(1)^2+8xx1+C_3#
#=>C_3=-2#
This gives us the expression for velocity as
#v=-2t^2+8t-2# .......(3)
and#v_(t=2)=(-2(2)^2+8xx2-2)#
#=>v_(t=2)=6\ ms^-1# ...........(6)
