What are the polar coordinates of $(6, - 6)$ $(6, -6)$ ?

Question

What are the polar coordinates of $(6, - 6)$ $(6, -6)$ ?

1 Answer

Impact of this question

3773 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-01-09T00:20:15

$(6 \sqrt{2}, - \frac{π}{4})$ $(6sqrt2,-pi/4)$

Explanation:

Polar coordinates are in the form $(r, θ)$ $(r,theta)$ .

$r$ $r$ is the radius and $θ$ $theta$ is the angle.

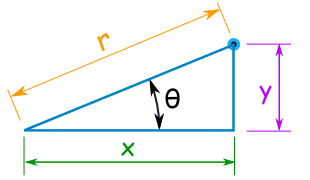
www.mathsisfun.com

Since $r$ $r$ is the hypotenuse of a right triangle, use the Pythagorean theorem to say that $r = \sqrt{x^{2} + y^{2}}$ $r=sqrt(x^2+y^2)$ .

To determine $θ$ $theta$ , you can say that $tan θ = \frac{y}{x}$ $tantheta=y/x$ , so $θ = {tan}^{- 1} (\frac{y}{x})$ $theta=tan^-1(y/x)$ .

Thus,

$r = \sqrt{6^{2} + {(- 6)}^{2}} = \sqrt{72} = 6 \sqrt{2}$ $r=sqrt(6^2+(-6)^2)=sqrt72=6sqrt2$

$θ = {tan}^{- 1} (\frac{6}{- 6}) = {tan}^{- 1} (- 1) = - \frac{π}{4}$ $theta=tan^-1(6/(-6))=tan^-1(-1)=-pi/4$

Note that the radian angle $- \frac{π}{4}$ $-pi/4$ will take us to Quadrant $IV$ $"IV"$ , which is where the original point $(6, - 6)$ $(6,-6)$ is.

The polar point is $(6 \sqrt{2}, - \frac{π}{4})$ $(6sqrt2,-pi/4)$ .

Science

Math

Humanities

... and beyond

What are the polar coordinates of $(6, - 6)$ $(6, -6)$ ?

1 Answer

Explanation:

Related questions

Impact of this question

Science

Math

Humanities

... and beyond

What are the polar coordinates of (6, -6)(6,−6)(6, -6)?

1 Answer

Explanation:

Related questions

Impact of this question

What are the polar coordinates of $(6, - 6)$ $(6, -6)$ ?