Question

What is the distance between `(9, 2, 0)` and `(4, 3, 1)`?

Answer 1

`sqrt((9 - 4)^2 + (2 - 3)^2 + (0 - 1)^2) = sqrt(5^2 + 1^2 + 1^2) = 3sqrt3`

Explanation:

The 2D Pythagorean Theorem states that

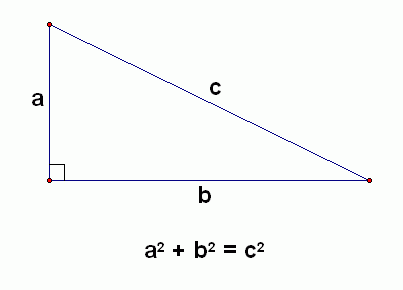
Now consider a 3D cuboid.

![http://demonstrations.wolfram.com/PythagoreanTheorem3D/]()

Applying the 2D Pythagorean Theorem twice gives

`d^2 = a^2 + z^2 = (x^2 + y^2) + z^2 = x^2 + y^2 + z^2`

Substituting the values `x=5`, `y=1`, `z=1` gives

`d^2 = 5^2 + 1^2 + 1^2 = 27`

`d = sqrt27 = 3sqrt3`

Answer 2

`3sqrt(3)`

Explanation:

The distance between any two points given the rectangular coordinates of the points is:
`color(white)("XX")`the square root of
`color(white)("XXXX")`the sum of
`color(white)("XXXXXX")`the squares of
`color(white)("XXXXXXXX")`the difference between each corresponding pair of coordinates.

In this case we have
`{: ("point A",color(white)("XX"),"(",9,",",color(white)("X")2,",",color(white)("X")0,")"), ("point B",color(white)("XX"),"(",4,",",color(white)("X")3,",",color(white)("X")1,")"), ("difference",color(white)("XX"),"(",5,",",-1,",",-1,")"), ("square of diff",color(white)("XX"),"(",25,",",color(white)("X")1,",",color(white)("X")1,")") :}`

distance `=sqrt(25+1+1) =sqrt(27)=3sqrt(3)`