What is the slope-intercept form of #10x - 5y = -2 #?
2 Answers
Explanation:
We know that slope-intercept form is:
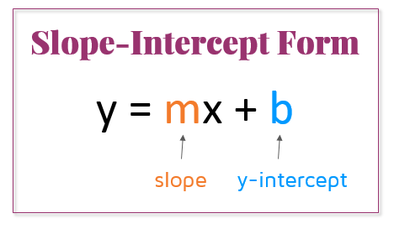
To make the equation in this form, find
Subtract
Divide both sides by
As you can see, this matches the slope-intercept form in the image.
Hope this helps!
Explanation:
Recall the equation of a line in slope-intercept form
We essentially just want a
Lastly, we can divide both sides by
Now, our equation is in slope-intercept form, with slope
Hope this helps!


