How do you simplify cos(u+v)cosv+sin(u+v)sinvcos(u+v)cosv+sin(u+v)sinv?

1 Answer
Noah G
Sep 5, 2016

The expression can be simplified to cosucosu.

Explanation:

We need to start by expanding the cos(A + B)cos(A+B) and the sin(A + B)sin(A+B) using the sum and difference identities, as shown in the following image.

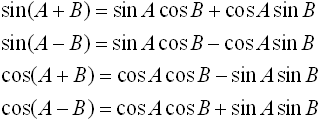
![http://www.regentsprep.org/regents/math/algtrig/att14/http://formulalesson.htm](https://useruploads.socratic.org/5YltLONvT86Xt1YrQQBu_formul30.gif)

Expanding, we have:

=>(cosucosv - sinusinv)(cosv) + (sinucosv + cosusinv)(sinv)⇒(cosucosv−sinusinv)(cosv)+(sinucosv+cosusinv)(sinv)

=>cosucos^2v - sinusinvcosv + sinucosvsinv + cosusin^2v⇒cosucos2v−sinusinvcosv+sinucosvsinv+cosusin2v

=>cosucos^2v + cosusin^2v⇒cosucos2v+cosusin2v

=>cosu(cos^2v + sin^2v)⇒cosu(cos2v+sin2v)

Applying the pythagorean identity sin^2x + cos^2x = 1sin2x+cos2x=1:

=>cosu⇒cosu

Hopefully this helps!

Related questions
See all questions in Sum and Difference Identities
Impact of this question
11456 views around the world
You can reuse this answer
Creative Commons License