How do you solve $tan (x + π) + 2 sin (x + π) = 0$ $tan(x+pi)+2sin(x+pi)=0$ ?

Question

How do you solve $tan (x + π) + 2 sin (x + π) = 0$ $tan(x+pi)+2sin(x+pi)=0$ ?

1 Answer

Impact of this question

13124 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-07-31T01:58:07

For this type of problem, you must use the double angle formulae to expand the parentheses.

Explanation:

The following formulas are extremely important. Be sure to retain them into the future.

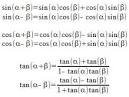
![http://study.com/academy/lesson/http://applying-the-sum-difference-identities.html](https://useruploads.socratic.org/20Hg8IkoTR6jDi9TFDpZ_images.jpeg)

Now, using these formulae, we can expand:

$\frac{tan (x) + tan (π)}{1 - tan x tan π} + 2 (sin x cos π + cos x sin π) = 0$ $(tan(x) + tan(pi))/(1 - tanxtanpi) + 2(sinxcospi + cosxsinpi) = 0$

$\frac{tan x + 0}{1 - tan x \times 0} + 2 (sin x (- 1) + cos x (0)) = 0$ $(tanx + 0)/(1 - tanx xx 0) + 2(sinx(-1) + cosx(0)) = 0$

$\frac{tan x}{1} + 2 (- sin x) = 0$ $tanx/1 + 2(-sinx) = 0$

$tan x - 2 sin x = 0$ $tanx - 2sinx = 0$

$\frac{sin x}{cos x} - 2 sin x = 0$ $sinx/cosx - 2sinx =0$

$\frac{sin x - 2 sin x cos x}{cos x} = 0$ $(sinx -2sinxcosx)/cosx = 0$

$sin x - 2 sin x cos x = 0 \times cos x$ $sinx - 2sinxcosx = 0 xx cosx$

$sin x (1 - 2 cos x) = 0$ $sinx(1 - 2cosx) = 0$

$sin x = 0 and cos x = \frac{1}{2}$ $sinx = 0 and cosx = 1/2$

$x = 0˚, 180˚, 60˚ and 300˚$

Note that these solutions are only in the interval $0˚ <= x <360˚$ .

Hopefully this helps!

Science

Math

Humanities

... and beyond

How do you solve $tan (x + π) + 2 sin (x + π) = 0$ $tan(x+pi)+2sin(x+pi)=0$ ?

1 Answer

Explanation:

Related questions

Impact of this question

Science

Math

Humanities

... and beyond

How do you solve tan(x+pi)+2sin(x+pi)=0tan(x+π)+2sin(x+π)=0tan(x+pi)+2sin(x+pi)=0?

1 Answer

Explanation:

Related questions

Impact of this question

How do you solve $tan (x + π) + 2 sin (x + π) = 0$ $tan(x+pi)+2sin(x+pi)=0$ ?