Question

What is the standard form of a polynomial `(5k + 2)(3k + 1)`?

Answer 1

`15k^2+11k+2=0`

Explanation:

Recall that the standard form of a polynomial is written in the form:

`color(teal)(|bar(ul(color(white)(a/a)ax^2+bx+c=0color(white)(a/a)|)))color(white)(X),color(white)(X)`where `a!=0`

For simplifying a quadratic equation into standard form, the F.O.I.L. (first, outside, inside, last) method is often used to expand the brackets. Here is what you will need to know before we start:


`1`. Assuming the given equation is equal to `0`, locate the terms, as well as their appropriate positive or negative signs.

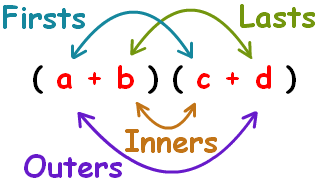
`(color(red)(5k)` `color(blue)(+2))(color(orange)(3k)` `color(green)(+1))=0`

`2`. For the "F" (first) in F.O.I.L., multiply `color(red)(5k)` and `color(orange)(3k)` together.

`color(red)(5k)(color(orange)(3k))`

`=color(purple)(15k^2)`

`3`. For the "O" (outside) in F.O.I.L., multiply `color(red)(+5k)` and `color(green)(1)` together.

`color(purple)(15k^2)` `color(red)(+5k)(color(green)1)`

`=color(purple)(15k^2)` `color(purple)(+5k)`

`4`. For the "I" (inside) in F.O.I.L., multiply `color(blue)(+2)` and `color(orange)(3k)` together.

`color(purple)(15k^2)` `color(purple)(+5k)` `color(blue)(+2)(color(orange)(3k))`

`=color(purple)(15k^2)` `color(purple)(+5k)` `color(purple)(+6k)`

`5`. For the "L" (last) in F.O.I.L., multiply `color(blue)(+2)` and `color(green)(1)` together.

`color(purple)(15k^2)` `color(purple)(+5k)` `color(purple)(+6k)` `color(blue)(+2)color(green)((1))`

`=color(purple)(15k^2)` `color(purple)(+5k)` `color(purple)(+6k)` `color(purple)(+2)`

`6`. Simplify the equation.

`color(green)(|bar(ul(color(white)(a/a)15k^2+11k+2=0color(white)(a/a)|)))`