Question

How do you express `cos(pi/ 3 ) * cos (( pi) / 6 )` without using products of trigonometric functions?

Answer 1

The final answer is `sqrt3/4`

Explanation:

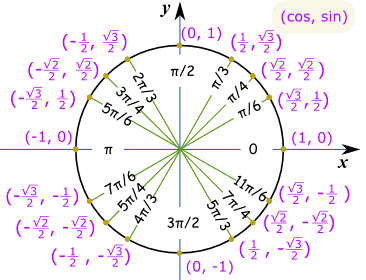
For Trig functions, here is your best friend, the trig circle.
What you see here is for every section of the circle you have, there is a value for the cosine and sine for that value.

Therefore if you look at the line of `pi/3` in the first quadrant, the cosine of `cos(pi/3)`, is equal to `1/2`

When you look at the line `pi/6` in the first quadrant, `cos(pi/6)` is equal to `sqrt3/2`

Then the multiplication of `cos(pi/3)*cos(pi/6)` is just multiplying simple fractions.

`1/2*sqrt3/2=sqrt3/4`