Products, Sums, Linear Combinations, and Applications

Key Questions

How do you use the transformation formulas to go from product to sum and sum to product?

Main approach to solve a trig equation : Use Trig Transformation Identities to transform it to a product of a few basic trig equations. Solving a trig equation finally results in solving a few basic trig equations.
Transformation Trig Identities that convert Sums to Products .
1. cos a + cos b = 2cos (a +b)/2cos (a - b)/2
2. cos a - cos b = -2sin (a + b)/2sin (a - b)/2
3. sin a + sin b = 2sin (a + b)/2cos (a - b)/2
4. sin a - sin b = 2cos (a + b)/2sin (a - b)/2
5. tan a + tan b = sin (a + b)/cos acos b.
6. tan a - tan b = sin (a - b)/cos acos b
Example 1 . Transform f(x) = sin a + cos a to a product.
Solution. Use Identity (3) to transform f(x) = sin a + sin (Pi/2 - a) = 2sin (Pi/4)sin (a + Pi/4)
Example 2 . Transform f(x) = sin x + sin 3x + sin 2x to a product. Use Identity (3) to transform the sum (sin x + sin 3x), then put in common factor.
f(x) = (2sin 2acos a) + 2sin acos a = 2cos a(2sin 3a/2*cos a/2)

Nghi N. · 3 · Apr 12 2015
How do you use linear combinations to solve trigonometric equations?

Answer:

Substitute

# a cos x + b sin x = sqrt{a^2 + b^2} cos(x -text{arctan2}( b //, a) ) #

where arctan2 is the two parameter, four quadrant inverse tangent.

Explanation:

I've been answering all these old math questions. It's hard to know if anyone reads the answers.

The linear combination of a cosine and a sine of the same angle corresponds to a scaling and a phase shift. Let's explain how that works.

The linear combination of a cosine and a sine of the same angle is an expression of the form:

# a cos x + b sin x #

That looks very much like the sum angle formula for sine or the difference angle formula for cosine:

# sin(alpha + beta ) = sin alpha cos beta + cos alpha sin beta #

# cos(alpha - beta) = cos alpha cos beta + sin alpha sin beta#

Indeed, we can take our linear combination and transform it into a scaled version of either of these. Pro Tip: When given a choice, prefer cosine to sine.

Let's multiply by a scale factor #r# and set #alpha = x, beta=theta.#

# r cos(x - theta) = r cos theta cos x + r sin theta sin x#

Matching to our linear combination leads us to want to solve for #r# and #theta#:

#a = r cos theta#

#b = r sin theta#

We've seen this before. It's how we turn turn the polar coordinates #P(r, theta)# to rectangular coordinates, here #(a,b).# So our task is to turn #(a,b)# to polar coordinates.

Let's remind ourselves how to do that, perhaps in a bit more detail than usually seen.

Squaring and adding we get

#a^2 + b^2 = (r cos theta)^2 + (r sin theta)^2 = r^2(cos^2 theta + sin^2 theta) = r^2#

# r = sqrt{a^2 + b^2}#

#sin theta = b/r#

#cos theta = a/r#

#tan theta = b/a#

#theta = text{arctan2}( b //, a)#

Usually this is written as the regular arctangent, but that's not really right. The regular arctangent only covers two quadrants, and doesn't work on the y axis. This is the two parameter, four quadrant inverse tangent, which returns a valid theta for all real input pairs. The #//,# is deliberate, reminding us there are two separate parameters, and which is which.

So now we're assured #a = r cos theta# and #b = r sin theta# so

# a cos x + b sin x = r cos theta cos x + r sin theta sin x = r cos(x - theta) #

# a cos x + b sin x = sqrt{a^2 + b^2} cos(x -text{arctan2}( b //, a) ) #

Dean R. · 1 · Apr 27 2018
How do you apply trigonometric equations to solve real life problems?

Answer:

When at #(71.06047^circ W, 43.08350^circ N) # a distant cell tower is at heading # 131^circ (SE)#, and at #(71.06137^circ W, 43.08007^circ N)# it's at heading #99^circ (E)#. Where is the tower?

Explanation:

Someone from San Antonio requested an answer three years ago! Hope they've figured it out by now.

Here some real life trig I've been meaning to do. I wanted to know where that cell phone tower I can see from my house is. It's on a hill in the distance.

From one spot near my house, maybe the one in this picture, I pointed my phone at the tower with my GPS app on and got this:

The relevant information is:

#(71.06047^circ W, 43.08350^circ N) # heading # 131^circ (SE)#

At another spot I got

#(71.06137^circ W, 43.08007^circ N)# heading #99^circ (E)#

The heading is relative to due north. Here's a figure.

We treat west as negative. I translated the origin to #(-71.06, 43,08) and multiplied the coordinates by 100,000 so our new problem is:

#(-047, 350) # heading # 131^circ (SE)#

#(-137, 007)# heading #99^circ (E)#

Find Tower coordinates #(x,y)#

To solve we write the equations of the two lines and find the meet.

When measured relative to the y axis like that, the heading angle #theta# converts to a slope as #m = cot theta#.

So our two lines

#y - 350 = (x+47) cot 131 #

#(y - 7)= (x+137) cot 99#

meet when

# 350 + (x+47) cot 131 = 7+ (x+137) cot 99 #

# x= {7 + 137 cot 99 -350 - 47 cot 131} /{cot 131 - cot 99} # x

# x≈ 455.537#

#y ≈-86.849 #

That means my tower is at GPS coordinates

# (-71.06 +.00456, 43.08 - .000868) = (-71.0554, 43.07132)#

Let's check Google Maps. Pretty good, off by around 400 feet.

Dean R. · 2 · Apr 27 2018
What is the sum to product formulas?

Answer:

As below.

Explanation:

#color(blue)("Sum to Product Formulas"#

()

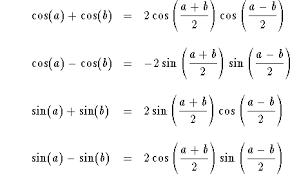#color(green)("Product to Sum Formulas"#

()

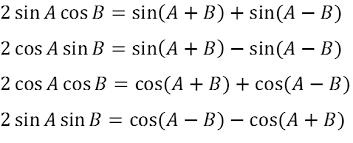sankarankalyanam · 1 · Mar 19 2018